练习册

  • 练习册
  • 试题
    精英家教网 > 高中物理 > 题目详情

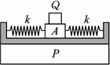
    某同学设计了一个测量物体质量的装置，如图所示，其中P是光滑水平面，k是轻质弹簧，A是质量为M、带夹子的标准质量金属块，Q是待测质量的物体，已知该装置的弹簧振子做简谐振动的周期为T＝2π，其中，m是振子的质量，k是与弹簧的劲度系数有关的常数，当只有A物体时，测得其振动周期为T1，将待测物体Q固定在A上面后，振动周期为T2，则待测物体的质量为_________．

    答案：
    解析：

    　　答案：

    　　解析：只有标准金属块A时，

    　　T1＝　　①

    　　当振子为Q与A的整体时(设Q的质量为m0)有

    　　T2＝　　②

    　　用①比②得：，整理得

    　　


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中物理 来源： 题型：

    某同学设计了一个测量物体质量的装置，如图所示，其中P是光滑水平面，A是质量为M的带夹子的已知质量金属块，Q是待测质量的物体（可以被A上的夹子固定）．已知该装置的弹簧振子做简谐运动的周期为T=2π
    m
    k
    （数量级为100s），其中m是振子的质量，K是与弹簧的劲度系数有关的常数．
    （1）为了达到实验目的还需要提供的实验器材是：
    秒表
    秒表
    ；
    （2）简要写出测量方法及所需测量的物理量（用字母表示）
    ①
    不放Q时用秒表测出振子振动30次的时间t1；（或者测出振子的周期T1）
    不放Q时用秒表测出振子振动30次的时间t1；（或者测出振子的周期T1）
    ；
    ②
    将Q固定在A上，用秒表测出振子振动30次的时间t2（或者测出振子的周期T2
    将Q固定在A上，用秒表测出振子振动30次的时间t2（或者测出振子的周期T2
    ；
    （3）用所测物理量和已知物理量求解待测物体质量的计算式为m=
    t22-t12
    t12
    M    或
    T22-T12
    T12
    M    ；
    t22-t12
    t12
    M    或
    T22-T12
    T12
    M    ；
    ；
    （4）如果这种装置与天平都在太空站中使用，则
    B
    B

    A．这种装置不能用来测质量，天平仍可以用来测质量
    B．这种装置仍可以用来测质量，天平不能用来测质量
    C．这种装置和天平都可以用来测质量
    D．这种装置和天平都不能用来测质量．

    查看答案和解析>>

    科目：高中物理 来源： 题型：

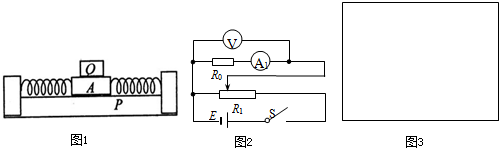
    （2012?怀化二模）在研究性学习中，某同学设计了一个测量导电纸的导电膜厚度的实验，该同学从资料上查得导电纸导电膜材料的电阻率为ρ，并利用下列器材完成了这个实验：
    A．电源E（电动势为12V，内阻不计）
    B．木板N（板上放有导电纸一张，导电膜向上），两个金属条a、b（平行放置在导电纸上，与导电纸接触良好，用作电极，其电极长度与导电纸宽度相同）
    C．滑线变阻器R（其总阻值小于两平行电极间导电纸的电阻）
    D．毫米刻度尺
    E．电压表V（量程为6V，内阻约3kΩ）
    F．电流表A（量程为0.6A，内阻忽略不计）
    G．开关K，导线若干．
    ①请用上述器材设计实验电路．在虚线框中画出实验电路原理图．
    ②实验中应测定的物理量是：
    导电膜的长度L1、宽度L2、电压表示数U、电流表示数I
    导电膜的长度L1、宽度L2、电压表示数U、电流表示数I
    ．
    ③计算导电膜厚度h的公式是：
    h=
    ρL1I
    L2U
    h=
    ρL1I
    L2U
    ．（用ρ和测得物理量的符号表示）

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    精英家教网（1）某同学设计了一个测量物体质量的装置，如图1所示，其中P是光滑水平轨道，A是质量为M的带夹子的已知质量金属块，Q是待测质量的物体（可以被A上的夹子固定）．已知该装置的弹簧振子做简谐运动的周期为T=2π
    		m/k
    ，其中m是振子的质量，k是与弹簧的劲度系数有关的常数．
    ①简要写出测量方法及所需测量的物理量（用字母表示）
    A．
     

    B．
     

    ②用所测物理量和已知物理量求解待测物体质量的计算式为m=
     
    ．
    （2）物体因绕轴转动而具有的动能叫转动动能，转动动能的大小与物体转动的角速度有关．如图2所示，为了研究某一砂轮的转动动能Ek与角速度ω和关系，可采用下述方法：先让砂轮由动力带动匀速旋转，测行其角速度ω，然后让砂轮脱离动力，由于克服转轴间摩擦力做功，砂轮最后停下．测出脱离动力到停止转动砂轮转过的转数n，测得几组不同的ω和n如下表所示：
    ω（rad/s） 0.5 1 2 3 4
    N 5 20 80 180 320
    Ek（J）
    另外已测得砂轮转轴的直径为1cm，转轴间的摩擦力为
    10
    π
    N    ．
    ①试计算出每次脱离动力时砂轮的转动动能，并填入上表中
    ②试由上述数据推导出该砂轮转动动能Ek与角速度ω的关系式Ek=
     

    ③若脱离动力后砂轮角速度为2.5rad/s，则它转过45转后角速度为
     
    rad/s．

    查看答案和解析>>

    科目：高中物理 来源： 题型：阅读理解

    Ⅰ（1）某同学设计了一个测量物体质量的装置，如图1所示，其中P是光滑水平面，A是质量为M的带夹子的已知质量金属块，Q是待测质量的物体．已知该装置的弹簧振子做简谐振动的周期为T=2π
    m
    k
    ，其中m是振子的质量，K是与弹簧的劲度系数有关的常数，当只有A物体振动时，测得其振动周期为T1，将待测物体Q固定在A上后，测得振动周期为T2，则待测物体的质量为
     
    ．
    精英家教网
    如果这种装置与天平都在太空站中使用，
    A．天平仍可以用来测质量，这种装置不能用来测质量
    B．这种装置仍可以用来测质量，天平不能用来测质量
    C．这种装置和天平都可以用来测质量
    D．这种装置和天平都不能用来测质量
    （2）某课题研究小组，收集了数码相机、手机等用旧了的各种类型的电池，及从废旧收音机上拆下的电阻、电容、电感线圈．现从这些材料中选取两个待测元件，一是电阻R0（约为2kΩ），二是手机中常用的锂电池（电动势E标称值为3.7V，允许最大放电电流为100mA）．在操作台上还准备了如下实验器材：
    A．电压表V（量程4V，电阻RV约为4.0kΩ）
    B．电流表A1（量程100mA，电阻RA1约为5Ω）
    C．电流表A2（量程2mA，电阻RA2约为50Ω）
    D．滑动变阻器R1（0～20Ω，额定电流1A）
    E．电阻箱R2（0～999.9Ω，最小分度值0.1Ω）
    F．开关S一只、导线若干
    Ⅱ（1）为了测定电阻R0的阻值，小组的一位成员，设计了如图2所示的电路原理图并选取了相应的器材（电源用待测的锂电池），其设计或器材选取中有不妥之处，你认为应该怎样调整？
     
    ．
    （2）在实际操作过程中，发现滑动变阻器R1、电流表A1已损坏，请用余下的器材测量锂电池的电动势E和内阻r．
    ①请你在图3方框中画出实验电路图（标注所用器材符号）
    ②为了便于分析，一般采用线性图象处理数据，请写出与线性图象对应的相关物理量间的函数关系式
     
    ．

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    某同学设计了一个测量金属丝电阻率的实验方案，实验室提供的器材有：
    A．电流表G（内阻Rg=99Ω，满偏电流Ig=3mA）
    B．电流表A（内阻约为0.2Ω，量程为0?0.6A）
    C．螺旋测微器
    D．电阻箱R0（0-9999Ω，0.5A）
    E．滑动变阻器R（5Ω，2A）
    F．干电池组（6V，0.05Ω）
    G．一个开关和导线若干
    他进行了以下操作：
    （1）用多用电表粗测金属丝的阻值：当用“x1OΩ”挡时发现指针偏转角度过大，他应该换用
     
    挡（填“x1Ω”或“x1OOΩ”），换挡并进行一系列正确操作后，指针静止时如图1所示，则金属丝的阻值约为
     
    Ω．
    （2）该同学为了较精确测量金属丝的阻值，设计了如图2实验电路，其中将电流表G 与电阻箱串联改装成量程为0～3V的电压表，则电阻箱的阻值应调为R0=
     
    Ω．请根据提供的器材和实验需要，将该同学设计的电路图补画完整．
    （3）实验数据的测量与电阻率的计算，如果金属丝的长度用L表示，直径用d表示，电路闭合后，调节滑动变阻器的滑片到合适位置，电流表C的示数为I1，电流表A的 示数为I2，请用已知量和测量量写出计算金属丝电阻率的表达式ρ
     
    ．精英家教网

    查看答案和解析>>

    同步练习册答案