
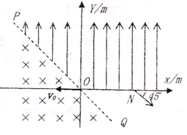
 如图所示,在xoy平面内,直线PQ平分第二、四象限(即与y轴成45°),直线PQ左侧空间存在着垂直纸面向里的匀强磁场,PQ上侧且y>0空间存在着沿y轴正方向的匀强电场,场强大小为E=10V/m;一个比荷$\frac{q}{m}$=103C/kg的带负电的粒子(重力不计),从坐标原点O以v0=200m/s的速度沿着x轴负方向进入匀强磁场,粒子从O点入射后,最后从x轴上N点射出电场,方向恰好与x轴正方向成45°,求:
如图所示,在xoy平面内,直线PQ平分第二、四象限(即与y轴成45°),直线PQ左侧空间存在着垂直纸面向里的匀强磁场,PQ上侧且y>0空间存在着沿y轴正方向的匀强电场,场强大小为E=10V/m;一个比荷$\frac{q}{m}$=103C/kg的带负电的粒子(重力不计),从坐标原点O以v0=200m/s的速度沿着x轴负方向进入匀强磁场,粒子从O点入射后,最后从x轴上N点射出电场,方向恰好与x轴正方向成45°,求:分析 (1)带电粒子在磁场中做圆周运动,根据左手定则判断出偏转的方向,然后画出运动的轨迹,即可确定;
(2)最后从x轴上N点射出电场,方向恰好与x轴正方向成45°,结合速度的分解,求出y方向的高度,从而确定粒子在磁场中运动的半径,最后又洛伦兹力提供向心力即可求出磁感应强度;
(3)粒子进入电场后做类平抛运动,根据轨迹求出微粒抛出点的高度和电场力产生的加速度,由运动的合成与分解求解微粒进入电场后在电场中运动的水平位移和时间.
解答 解:(1)微粒在磁场中受洛伦兹力作用下做匀速圆周运动,画出轨迹如图,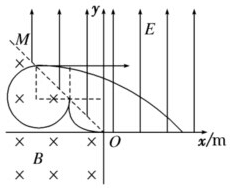
可知,粒子先做$\frac{1}{4}$圆周运动,然后在电场中在电场力作用下先向上匀减速然后向下匀加速,
离开电场时速度大小与进入时大小相等.然后在磁场中做$\frac{3}{4}$圆周运动,最后以垂直于电场方向的速度再进入电场作类平抛运动.
所以,粒子第一次经过直线PQ时速度的大小仍然是200m/s,方向竖直向上.
(2)粒子在电场中的加速度:a=$\frac{qE}{m}=1{0}^{3}×10=1{0}^{4}$m/s2,
粒子第二次离开磁场在电场中做类平抛运动时抛出点高度h=2R,所以粒子在竖直方向做初速度为0的匀加速直线运动,故沿电场方向的分速度:
vy=at2
由于粒子从x轴上N点射出电场,方向恰好与x轴正方向成45°,所以:vy=v0tan45°=v0=200m/s
得:${t}_{2}=\frac{{v}_{y}}{a}=\frac{200}{1{0}^{4}}=0.02$s
有:h=$\frac{1}{2}$$a{t}_{2}^{2}$=$\frac{1}{2}×1{0}^{4}×0.0{2}^{2}m=2$m,
则R=1m
粒子在磁场中运动,洛伦兹力提供向心力,得:$q{v}_{0}B=\frac{m{v}_{0}^{2}}{R}$
所以:B=$\frac{m{v}_{0}}{qR}=\frac{200}{1{0}^{3}×2}T=0.2$T
(3)粒子在水平方向的位移:x=v0t2=200×0.02m=4m
结合几何关系可知,N点的位移:xN=x-2R=4m-2×1m=2m
粒子第一次经过直线PQ时速度的大小仍然是200m/s,方向竖直向上,粒子先向上匀减速然后向下匀加速,运动的时间:
${t}_{1}=\frac{△v}{a}=\frac{2{v}_{0}}{a}=\frac{2×200}{1{0}^{4}}s=0.04$s
可得粒子在电场中运动时间:t=t1+t2=0.04s+0.02s=0.06s,
答:(1)粒子第一次经过直线PQ时速度的大小是200m/s,方向竖直向上;
(2)磁感应强度B的大小是0.2T;
(3)N点离O点的距离是2m,粒子在电场中的时间是0.6s.
点评 解决本题的关键是掌握带电微粒在匀强磁场中做匀速圆周运动,知道周期及半径公式,微粒在电场中可以做匀变速直线运动或抛体运动,熟练掌握运动规律是解决问题的基础.


科目:高中物理 来源: 题型:选择题
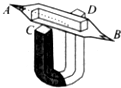 如图所示是用阴极射线管演示电子在磁场中受洛伦兹力的实验装置,图中虚线是电子的运动轨迹,那么下列关于此装置的说法正确的是( )
如图所示是用阴极射线管演示电子在磁场中受洛伦兹力的实验装置,图中虚线是电子的运动轨迹,那么下列关于此装置的说法正确的是( )| A. | A端接的是高压直流电源的正极 | B. | C端是蹄形磁铁的N极 | ||
| C. | C端是蹄形磁铁的S极 | D. | 以上说法均不对 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
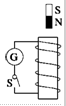 如图所示,闭合开关S,将条形磁铁两次插入闭合线圈,第一次用0.2s,第二次用0.4s,并且两次的起始和终止位置相同,则( )
如图所示,闭合开关S,将条形磁铁两次插入闭合线圈,第一次用0.2s,第二次用0.4s,并且两次的起始和终止位置相同,则( )| A. | 第一次磁通量变化较大 | |
| B. | 第一次 的最大偏角较大 的最大偏角较大 | |
| C. | 第一次经过 的总电量较多 的总电量较多 | |
| D. | 若断开开关S, 均不偏转,故均无感应电动势 均不偏转,故均无感应电动势 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 一质量为m的滑块(视为质点),从水平面上与一平面相切与A点以V0=$\sqrt{8Rg}$的速度进入竖直半圆形轨道开始作圆周运动,轨道半径为R,经半圆轨道的最高点B飞出,落回到水平面上的C点,如图所示,若AC=2AB=4R
一质量为m的滑块(视为质点),从水平面上与一平面相切与A点以V0=$\sqrt{8Rg}$的速度进入竖直半圆形轨道开始作圆周运动,轨道半径为R,经半圆轨道的最高点B飞出,落回到水平面上的C点,如图所示,若AC=2AB=4R查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,在水平面上固定着三个完全相同的木块,一子弹以水平速度v0射入木块,若子弹在木块中做匀减速直线运动,当穿透第三个木块时速度恰好为零,则子弹依次射入每个木块时的速度v1、v2、v3之比和穿过每个木块所用的时间t1、t2、t3之比分别为( )
如图所示,在水平面上固定着三个完全相同的木块,一子弹以水平速度v0射入木块,若子弹在木块中做匀减速直线运动,当穿透第三个木块时速度恰好为零,则子弹依次射入每个木块时的速度v1、v2、v3之比和穿过每个木块所用的时间t1、t2、t3之比分别为( )| A. | v1:v2:v3=1:2:3 | B. | v1:v2:v3=$\sqrt{3}:\sqrt{2}$:1 | ||
| C. | t1:t2:t3=1:$\sqrt{2}:\sqrt{3}$ | D. | t1:t2:t3=($\sqrt{3}$-$\sqrt{2}$):($\sqrt{2}$-1):1 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,弹簧下端悬一滑轮,跨过滑轮的细线两端系有A、B两重物,mB=2kg,不计线、滑轮质量及摩擦,将A、B两重物由静止释放后,弹簧的示数不可能为:(g=10m/s2)( )
如图所示,弹簧下端悬一滑轮,跨过滑轮的细线两端系有A、B两重物,mB=2kg,不计线、滑轮质量及摩擦,将A、B两重物由静止释放后,弹簧的示数不可能为:(g=10m/s2)( )| A. | 40N | B. | 60N | C. | 70N | D. | 100N |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
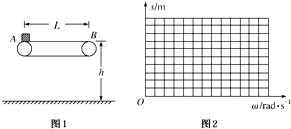 如图1所示为车站使用的水平传送带的模型,它的水平传送带AB的长度为L=8m,传送带的皮带轮的半径均为R=0.2m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(可视为质点)以初速度v0=10m/s水平地滑上水平传送带A端.已知旅行包与传送带之间的动摩擦因数为μ=0.6,皮带轮与皮带之间始终不打滑,g取10m/s2.讨论下列问题:
如图1所示为车站使用的水平传送带的模型,它的水平传送带AB的长度为L=8m,传送带的皮带轮的半径均为R=0.2m,传送带的上部距地面的高度为h=0.45m,现有一个旅行包(可视为质点)以初速度v0=10m/s水平地滑上水平传送带A端.已知旅行包与传送带之间的动摩擦因数为μ=0.6,皮带轮与皮带之间始终不打滑,g取10m/s2.讨论下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com