额定功率为80KW的汽车,在某平直的公路上行驶的最大速度为20m/s,汽车的质量m=2×103kg.如果汽车从静止开始做匀加速直线运动,加速度大小为2m/s2,运动过程中阻力不变,求:
(1)汽车所受的恒定阻力是多大
(2)3秒末汽车瞬时功率是多大.
解:(1)当牵引力等于阻力时,速度达到最大值,又根据p=Fv可知:
f=F=

=

N=4000N
(2)汽车在达到额定功率前做匀加速直线运动,设匀加速运动的时间为t,达到额定功率时速度为v,
由a=

得:F=8000N
由p=Fv得 v=10m/s
t=
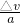
=
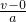
=5s
因为3s<5s
所以3s末汽车仍做匀加速直线运动,故v
3=at
3=6m/s
所以p
3=FV
3=48KW
答:汽车所受的恒定阻力是4000N;3秒末汽车瞬时功率是48KW.
分析:这题考的知识点是汽车的两种启动方式,恒定加速度启动和恒定功率启动.本题属于恒定加速度启动方式,由于牵引力不变,根据p=Fv可知随着汽车速度的增加,汽车的实际功率在增加,此过程汽车做匀加速运动,当实际功率达到额定功率时,功率不能增加了,要想增加速度,就必须减小牵引力,当牵引力减小到等于阻力时,加速度等于零,速度达到最大值.求3s末的瞬时功率,首先要知道3s末时汽车是否还处于匀加速直线运动的状态.
点评:本题考查的是机车启动的两种方式,即恒定加速度启动和恒定功率启动.要求同学们能对两种启动方式进行动态分析,能画出动态过程的方框图,公式p=Fv,p指实际功率,F表示牵引力,v表示瞬时速度.当牵引力等于阻力时,机车达到最大速度
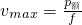
.

 =
= N=4000N
N=4000N 得:F=8000N
得:F=8000N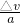 =
=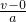 =5s
=5s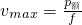 .
. 
