实验用弹射器的子弹从枪口射出时的速度大小是30m/s,弹射器每隔1s竖直向上开一枪.假定子弹在上升过程中都不相碰且枪口离地面的高度忽略不计,不计空气阻力,取g=10m/s2.
(1)求空中最多能有几颗子弹?
(2)设在t=0时,将第一颗子弹射出,则在哪些时刻它和以后射出的子弹在空中相遇而过?
(3)这些子弹在距射出点多高的地方依次与第一颗子弹相遇?
【答案】
分析:(1)计算出第一颗子弹在空中停留的总时间,便可知道空中最多能有几颗子弹
(2)子弹相遇时,它们对地面的位移相等,列位移相同的方程讨论解决相遇的时间
(3)依据第二问的结果,计算出第一颗子弹的对地位移,可得本问的结果
解答:解:(1)第一颗子弹从射出到落回地面共用时间:t=
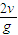
=6s
因每隔1s发出一颗子弹,故第一颗子弹落地时,第七颗子弹刚发出,空中共有6颗子弹
(2)设第一颗子弹射出时间t后,与第n颗子弹相遇,此时第n颗子弹运动时间:
t
n=t-n+1
由运动学公式得,v
t-

gt
2=v
t
n-

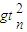
解得:t=3+

(n-1)
当n=2时,t=3.5s
当n=3时,t=4.0s
当n=4时,t=4.5s
当n=5时,t=5.0s
当n=6时,t=5.5s
(3)设第一颗子弹与第n颗子弹相遇时距射出点的高度为h,则有:
h
n=v
t
n-

g
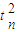
所以,h
2=43.75m,h
3=40m,h
4=33.75m,h
5=25m,h
6=13.75m
答:(1)空中最多有6颗子弹
(2)在3.5s,4.0s,4.5s,5.0s,5.5s第一颗子弹与其他子弹相遇
(3)相遇点高度为:43.75m,40m,33.75m,25m,13.75m
点评:相遇的条件是位移相等,这一点必须把握;其次,列通式方程讨论解决问题是物理学中多解问题常用的方法,要注意加强训练

 =6s
=6s gt2=vtn-
gt2=vtn-
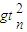
 (n-1)
(n-1) g
g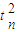


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案