
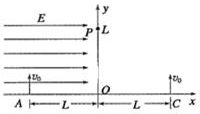
 为了观察正、负电子的碰撞现象,有人设想利用电场、磁场控制正、负电子在云室中运动来实现这一过程.在如图所示的xOy平面内,A、C二小孔距原点的距离均为L,每隔一定的时间源源不断地分别从A孔射入正电子,C孔射入负电子,初速度均为v0,且垂直x轴,正、负电子的质量均为m,电荷量均为e(忽略电子之间的相互作用).在y轴的左侧区域加一水平向右的匀强电场,在y轴的右侧区域加一垂直纸面的匀强磁场(图中未画出),要使正、负电子在y轴上的P(0,L)处相碰,求:
为了观察正、负电子的碰撞现象,有人设想利用电场、磁场控制正、负电子在云室中运动来实现这一过程.在如图所示的xOy平面内,A、C二小孔距原点的距离均为L,每隔一定的时间源源不断地分别从A孔射入正电子,C孔射入负电子,初速度均为v0,且垂直x轴,正、负电子的质量均为m,电荷量均为e(忽略电子之间的相互作用).在y轴的左侧区域加一水平向右的匀强电场,在y轴的右侧区域加一垂直纸面的匀强磁场(图中未画出),要使正、负电子在y轴上的P(0,L)处相碰,求:分析 (1)正电子进入电场后做类平抛运动,由牛顿第二定律和位移时间公式结合,即可求解电场强度E的大小.负电子进入磁场后做匀速圆周运动,由题可知轨迹半径等于L,由牛顿第二定律和向心力公式结合求解B的大小,由左手定则判断B的方向.
(2)正电子在电场中运动时,电场力对其做正功,由动能定理求出相碰前正电子的动能,由其竖直方向做匀速直线运动的规律,求解其运动时间,而负电子在磁场中运动时洛伦兹力不做功,动能不变,根据时间为$\frac{1}{4}$周期,从而可求出时间差.
解答 解:(1)对A处进入的正电子,由类平抛运动规律得:
水平方向:L=v0tA,竖直方向:L=$\frac{1}{2}$atA2=$\frac{eE}{2m}$tA2.解得:E=$\frac{2m{v}_{0}^{2}}{2eL}$;
对C处进入的负电子,由牛顿第二定律得:
ev0B=m$\frac{{v}_{0}^{2}}{L}$,解得:B=$\frac{m{v}_{0}}{eL}$,
负电子在C点所受的洛伦兹力向左,由左手定则判断可知磁场B的方向垂直纸面向外.
(2)对A处进入的正电子,由动能定理得:
EeL=EkA-$\frac{1}{2}$mv02,所以 EkA=$\frac{5m{v}_{0}^{2}}{2}$,
而 EkB=$\frac{1}{2}$mv02,故 $\frac{{E}_{KA}}{{E}_{KB}}$=$\frac{5}{1}$,
从C进入的负电子运动的时间为:tB=$\frac{90°}{360°}$×$\frac{2πL}{{v}_{0}}$=$\frac{πL}{2{v}_{0}}$,
正电子在电场中运动的时间为:tA=$\frac{L}{{v}_{0}}$
则△t=tB-tA=$\frac{(π-2)L}{2{v}_{0}}$;
答:(1)电场强度E的大小为$\frac{2m{v}_{0}^{2}}{2eL}$;磁感应强度B的大小为$\frac{m{v}_{0}}{eL}$,方向:垂直于纸面向外;
(2)P点相碰的正、负电子的动能之比和射入小孔的时间差△t为$\frac{(π-2)L}{2{v}_{0}}$.
点评 本题考查了粒子在电场与磁场中的运动,解决本题的关键是抓住电场中偏转与磁场中偏转研究方法的不同,运用动力学方法处理.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:多选题
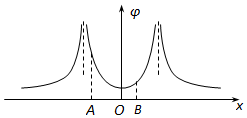 某静电场在x轴上各点的电势φ随坐标x的分布图象如图.x轴上A、O、B三点的电势值分别为φA、φO、φB,电场强度沿x轴方向的分量大小分别为EAx、EOx、EBx,电子在A、O、B三点的电势能分别为EPA、EPO、EPB.下列判断正确的是( )
某静电场在x轴上各点的电势φ随坐标x的分布图象如图.x轴上A、O、B三点的电势值分别为φA、φO、φB,电场强度沿x轴方向的分量大小分别为EAx、EOx、EBx,电子在A、O、B三点的电势能分别为EPA、EPO、EPB.下列判断正确的是( )| A. | φO<φB<φA | B. | EOx<EBx<EAx | C. | EPO<EPB<EPA | D. | EPO-EPA>EPO-EPB |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
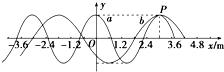 两列简谐横波a、b在同一种均匀介质中沿x轴传播,a波周期为0.5s.某时刻,两列波的波峰正好在xP=3.0m处的P点重合,如图甲所示,则b波的周期为Tb=0.8s,该时刻,离P点最近的波峰重叠点的平衡位置坐标是x=27.0或-21.0m.
两列简谐横波a、b在同一种均匀介质中沿x轴传播,a波周期为0.5s.某时刻,两列波的波峰正好在xP=3.0m处的P点重合,如图甲所示,则b波的周期为Tb=0.8s,该时刻,离P点最近的波峰重叠点的平衡位置坐标是x=27.0或-21.0m.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
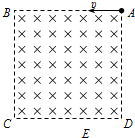 如图所示,边长为L的正方形区域ABCD内存在方向垂直纸面向里的匀强磁场,E点位于CD边上,且ED=$\frac{{\sqrt{3}}}{3}$L,三个完全相同的带电粒子1、2、3分别以大小不同的初速度υ1、υ2、υ3从A点沿AB方向射入该磁场区域,经磁场偏转后粒子1、2、3分别从C点、E点、D点射出.若t1、t2、t3分别表示粒子1、2、3在磁场中的运动时间.则以下判断正确的是( )
如图所示,边长为L的正方形区域ABCD内存在方向垂直纸面向里的匀强磁场,E点位于CD边上,且ED=$\frac{{\sqrt{3}}}{3}$L,三个完全相同的带电粒子1、2、3分别以大小不同的初速度υ1、υ2、υ3从A点沿AB方向射入该磁场区域,经磁场偏转后粒子1、2、3分别从C点、E点、D点射出.若t1、t2、t3分别表示粒子1、2、3在磁场中的运动时间.则以下判断正确的是( )| A. | υ1:υ2:υ3=6:2$\sqrt{3}$:3 | B. | υ1:υ2:υ3=4:3:2 | C. | t1:t2:t3=2:3:4 | D. | t1:t2:t3=3:4:6 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
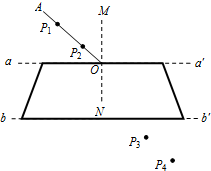 如图所示,在“用插针法测定玻璃的折射率”的实验中,一位同学已完成了部分实验操作,他在白纸上O点画出界面aa′的法线MN,并画出一条带箭头的线段AO作为入射光线.在入射光线上竖直地插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,在P3位置插的大头针正好挡住P1、P2的像,在P4位置插的大头针正好挡住大头针P3和大头针P1、P2的像.根据n=$\frac{sini}{sinr}$可计算出玻璃的折射率,请你在图中完成整个光路图,并标出入射角i和折射角r.
如图所示,在“用插针法测定玻璃的折射率”的实验中,一位同学已完成了部分实验操作,他在白纸上O点画出界面aa′的法线MN,并画出一条带箭头的线段AO作为入射光线.在入射光线上竖直地插上两枚大头针P1、P2,透过玻璃砖观察大头针P1、P2的像,在P3位置插的大头针正好挡住P1、P2的像,在P4位置插的大头针正好挡住大头针P3和大头针P1、P2的像.根据n=$\frac{sini}{sinr}$可计算出玻璃的折射率,请你在图中完成整个光路图,并标出入射角i和折射角r.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
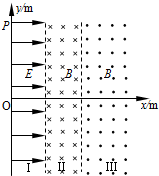 如图所示,空间被平行界面分为三个区域,Ⅰ区域存在匀强电场,电场强度E可取不同值,其左边界与y轴重合;Ⅱ区域磁场方向垂直纸面向里、Ⅲ区域磁场方向垂直纸面向外,磁感应强度均为B,Ⅰ、Ⅱ区域宽度均为d,Ⅲ区域右侧无限制;平面直角坐标系中点P(0,3d).质量m、电荷量+q粒子从坐标原点O由静止释放进入电场.粒子的重力不计.求:
如图所示,空间被平行界面分为三个区域,Ⅰ区域存在匀强电场,电场强度E可取不同值,其左边界与y轴重合;Ⅱ区域磁场方向垂直纸面向里、Ⅲ区域磁场方向垂直纸面向外,磁感应强度均为B,Ⅰ、Ⅱ区域宽度均为d,Ⅲ区域右侧无限制;平面直角坐标系中点P(0,3d).质量m、电荷量+q粒子从坐标原点O由静止释放进入电场.粒子的重力不计.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
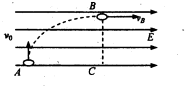 如图,一质量为m,电量+q的小球,以垂直于电场方向的速度v0竖直向上进入一个匀强电场,经过一段时间后,该小球的速度vB恰好与场强方向平行.若在此过程中水平位移是上升高度的2倍,即AC=2BC,则A、C两点间的电压是( )
如图,一质量为m,电量+q的小球,以垂直于电场方向的速度v0竖直向上进入一个匀强电场,经过一段时间后,该小球的速度vB恰好与场强方向平行.若在此过程中水平位移是上升高度的2倍,即AC=2BC,则A、C两点间的电压是( )| A. | $\frac{{mv}_{0}^2}{2q}$ | B. | $\frac{{2mv}_{0}^2}{q}$ | C. | $\frac{{mv}_{0}^2}{q}$ | D. | $\frac{{mv}_{0}^2}{4q}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
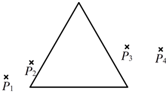 某同学测量一块玻璃三棱镜的折射率,经正确操作,插下了四枚大头针P1、P2和P3、P4,如图所示.
某同学测量一块玻璃三棱镜的折射率,经正确操作,插下了四枚大头针P1、P2和P3、P4,如图所示.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com