
 传送带在工农业生产中有着广泛的应用.如图所示,平台上的人欲通过一根平行于传送带的轻绳将物品拉上平台,已知物品质量m=50kg,可看成质点,用F=500N的恒力从静止开始往上拉,传送带与水平面的夹角θ=37°,从传送带底端到平台左边的距离L=2.25m,传送带以恒定速度v=2m/s顺时针运行,物品与传送带之间的动摩擦因数μ=0.5,设最大静摩擦力等于滑动摩擦力.(g取10m/s2,sin 37°=0.6,cos 37°=0.8)问:
传送带在工农业生产中有着广泛的应用.如图所示,平台上的人欲通过一根平行于传送带的轻绳将物品拉上平台,已知物品质量m=50kg,可看成质点,用F=500N的恒力从静止开始往上拉,传送带与水平面的夹角θ=37°,从传送带底端到平台左边的距离L=2.25m,传送带以恒定速度v=2m/s顺时针运行,物品与传送带之间的动摩擦因数μ=0.5,设最大静摩擦力等于滑动摩擦力.(g取10m/s2,sin 37°=0.6,cos 37°=0.8)问: 得:
得: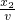 =1s
=1s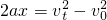



科目:高中物理 来源: 题型:
 传送带在工农业生产中有着广泛的应用.如图所示,平台上的人欲通过一根平行于传送带的轻绳将物品拉上平台,已知物品质量m=50kg,可看成质点,用F=500N的恒力从静止开始往上拉,传送带与水平面的夹角θ=37°,从传送带底端到平台左边的距离L=2.25m,传送带以恒定速度v=2m/s顺时针运行,物品与传送带之间的动摩擦因数μ=0.5,设最大静摩擦力等于滑动摩擦力.(g取10m/s2,sin 37°=0.6,cos 37°=0.8)问:
传送带在工农业生产中有着广泛的应用.如图所示,平台上的人欲通过一根平行于传送带的轻绳将物品拉上平台,已知物品质量m=50kg,可看成质点,用F=500N的恒力从静止开始往上拉,传送带与水平面的夹角θ=37°,从传送带底端到平台左边的距离L=2.25m,传送带以恒定速度v=2m/s顺时针运行,物品与传送带之间的动摩擦因数μ=0.5,设最大静摩擦力等于滑动摩擦力.(g取10m/s2,sin 37°=0.6,cos 37°=0.8)问:查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题

查看答案和解析>>
科目:高中物理 来源:2012-2013学年四川省凉山州会理一中高三(上)月考物理试卷(一)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com