
 如图所示,小物块A、B放置光滑水平面上,A的质量为2m,B的质量为m,A与B之间具有下列相互作用特性:当它们间的距离xAB≤x0时,始终存在一个恒定的引力F0;当xAB>x0时,相互作用力为零.
如图所示,小物块A、B放置光滑水平面上,A的质量为2m,B的质量为m,A与B之间具有下列相互作用特性:当它们间的距离xAB≤x0时,始终存在一个恒定的引力F0;当xAB>x0时,相互作用力为零.分析 (1)根据牛顿第二定律分别求出AB的加速度,再由位移关系求相遇时间;
(2)对AB由牛顿第二定律求出加速度,根据题意加速度相同,即可得出${F}_{1}^{\;}$的大小;
(3)求出AB的加速度,AB加速度不同,A的加速度大于B的加速度,求出AB间距离增大到${x}_{0}^{\;}$的时间,分段求出B的速度;
解答 解:(1)根据题意,当它们间的距离xAB≤x0时,始终存在一个恒定的引力${F}_{0}^{\;}$
对物体A:${a}_{A}^{\;}=\frac{{F}_{0}^{\;}}{2m}$ 对物体B:${a}_{B}^{\;}=\frac{{F}_{0}^{\;}}{m}$
${x}_{A}^{\;}+{x}_{B}^{\;}={x}_{0}^{\;}$
$\frac{1}{2}{a}_{A}^{\;}{t}_{\;}^{2}+\frac{1}{2}{a}_{B}^{\;}{t}_{\;}^{2}={x}_{0}^{\;}$
代入解得:$t=2\sqrt{\frac{m{v}_{0}^{\;}}{3{F}_{0}^{\;}}}$
(2)对物体A,有${F}_{1}^{\;}-{F}_{0}^{\;}=2m{a}_{A}^{\;}$①
对物体B,有${F}_{0}^{\;}=m{a}_{B}^{\;}$②
根据题意,加速度相等${a}_{A}^{\;}={a}_{B}^{\;}$③
联立解得:${F}_{1}^{\;}=3{F}_{0}^{\;}$
(3)根据题意,对A施加一水平向右的拉力F,且$F>3{F}_{0}^{\;}$
由(2)知,则A的加速度大于B的加速度
设经过时间${t}_{0}^{\;}$,AB之间的距离增大到${x}_{0}^{\;}$
对A,根据牛顿第二定律$F-{F}_{0}^{\;}=2m{a}_{A}^{\;}$
对B,根据牛顿第二定律${F}_{0}^{\;}=m{a}_{B}^{\;}$
${x}_{A}^{\;}-{x}_{B}^{\;}=\frac{{x}_{0}^{\;}}{2}$
$\frac{1}{2}\frac{F-{F}_{0}^{\;}}{2m}{t}_{0}^{2}-\frac{1}{2}\frac{{F}_{0}^{\;}}{m}{t}_{0}^{2}=\frac{{x}_{0}^{\;}}{2}$
解得:${t}_{0}^{\;}=\sqrt{\frac{2m{x}_{0}^{\;}}{F-3{F}_{0}^{\;}}}$
当$0<t≤\sqrt{\frac{2m{x}_{0}^{\;}}{F-3{F}_{0}^{\;}}}$时,${v}_{B}^{\;}={a}_{B}^{\;}t=\frac{{F}_{0}^{\;}}{m}t$
当$t>\sqrt{\frac{2m{x}_{0}^{\;}}{F-3{F}_{0}^{\;}}}$时,${v}_{B}^{\;}={a}_{B}^{\;}{t}_{0}^{\;}=\frac{{F}_{0}^{\;}}{m}\sqrt{\frac{2m{x}_{0}^{\;}}{F-3{F}_{0}^{\;}}}$
答:(1)若A、B由相距x0处静止释放,则经过时间$2\sqrt{\frac{m{x}_{0}^{\;}}{3{F}_{0}^{\;}}}$他们相遇
(2)若对A施加一水平向右的拉力F1,A、B以相同的加速度向右运动,拉力F1的大小为$3{F}_{0}^{\;}$;
(3)若t0=0时刻,A、B相距$\frac{{x}_{0}}{2}$,对A施加一水平向右的拉力F(F>3F0),使A、B由静止开始运动,t时刻B的速度
当$0<t≤\sqrt{\frac{2m{x}_{0}^{\;}}{F-3{F}_{0}^{\;}}}$时,${v}_{B}^{\;}=\frac{{F}_{0}^{\;}}{m}t$
当$t>\sqrt{\frac{2m{x}_{0}^{\;}}{F-3{F}_{0}^{\;}}}$时,${v}_{B}^{\;}=\frac{{F}_{0}^{\;}}{m}\sqrt{\frac{2m{x}_{0}^{\;}}{F-3{F}_{0}^{\;}}}$
点评 本题考查牛顿运动定律和运动学公式的应用,关键是注意分析受力情况,结合位移关系列式,注意距离大于${x}_{0}^{\;}$两球之间无作用力.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:高中物理 来源: 题型:多选题

| A. | 甲、乙两物体均做匀变速直线运动 | |
| B. | 甲、乙两物体由不同地点同时出发,t0时刻两物体相遇 | |
| C. | 0~t0时间内,乙的位移大于甲的位移 | |
| D. | 0~t0时间内,甲的速度大于乙的速度;t0时刻后,乙的速度大于甲的速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 使用如图(a)所示的装置验证机械能守恒定律,打出一条纸带如图(b)所示.图(b)中O是打出的第一个点迹,A、B、C、D、E、F…是依次打出的点迹,量出OE间的距离为L,DF间的距离为S,已知打点计时器打点的周期是T.
使用如图(a)所示的装置验证机械能守恒定律,打出一条纸带如图(b)所示.图(b)中O是打出的第一个点迹,A、B、C、D、E、F…是依次打出的点迹,量出OE间的距离为L,DF间的距离为S,已知打点计时器打点的周期是T.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 杀菌作用 | B. | 化学作用 | C. | 波长短 | D. | 能量高 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 半导体的导电性能介于导体和绝缘体之间 | |
| B. | 半导体的导电性能随温度的升高而减弱 | |
| C. | 半导体只能制成光敏元件 | |
| D. | 半导体可制成大规模集成电路 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
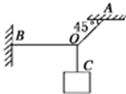 如图所示,能承受最大拉力为100N的细线OA与竖直方向成45°角,能承受最大拉力为5 0N的细线OB水平,细线OC能承受足够大的拉力,为使OA,OB均不被拉断,OC下端所悬挂物体的最大重力是多少?
如图所示,能承受最大拉力为100N的细线OA与竖直方向成45°角,能承受最大拉力为5 0N的细线OB水平,细线OC能承受足够大的拉力,为使OA,OB均不被拉断,OC下端所悬挂物体的最大重力是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com