
分析 1、根据自由落体运动$h=\frac{1}{2}{g}_{月}{t}^{2}$,代入数据化简可得重力加速度.
2、月球表面的重力等于月球对物体的万有引力,第一宇宙速度是环绕月球表面的匀速圆周运动,结合向心力的表达式即可求出.
3、根据万有引力提供向心力$G\frac{Mm}{{R}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}$即可求出.
解答 解:(1)由自由落体规律$h=\frac{1}{2}{g}_{月}{t}^{2}$
代入数据可得:${g}_{月}=1.6m/{s}^{2}$
(2)设月球径为R,绕月卫星质量为m,在月球的表面的重力等于万有引力:
$G\frac{Mm}{{R}^{2}}=m{g}_{月}$
设绕月轨道半径为R,绕月卫星质量为m,由牛顿第二定律
$G\frac{Mm}{{R}^{2}}=m\frac{{v}^{2}}{R}$
所以:$v=\sqrt{gR}=\sqrt{1.6R}$
(3)又由万有引力提供向心力,得:$G\frac{Mm}{{(R+h)}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}(R+h)$
可得T=$\frac{2π}{R}\sqrt{\frac{(R+h)^{3}}{g}}$
答:(1)月球表面的重力加速度g月为1.6m/s2.
(2)月球的第一宇宙速度v的表达式为v=$\sqrt{1.6R}$;
(3)若卫星绕月球做匀速圆周运动,运行轨道距离月面高度为h,卫星的运行周期为$\frac{2π}{R}\sqrt{\frac{(R+h)^{3}}{g}}$.
点评 解决本题的关键掌握自由落体运动的位移时间公式$h=\frac{1}{2}{g}_{月}{t}^{2}$和速度时间公式vy=g月t.环绕天体绕中心天体做匀速圆周运动,由中心天体的万有引力提供向心力.


科目:高中物理 来源: 题型:实验题
 如图所示为小球做自由落体运动时,用频闪照相得到的轨迹的一部分.已知闪光的时间间隔为1/30s,则小球运动到计时点2时的瞬时速度为2.47m/s;小球下落的加速度为9.45m/s2.(保留3位有效数字)
如图所示为小球做自由落体运动时,用频闪照相得到的轨迹的一部分.已知闪光的时间间隔为1/30s,则小球运动到计时点2时的瞬时速度为2.47m/s;小球下落的加速度为9.45m/s2.(保留3位有效数字)查看答案和解析>>
科目:高中物理 来源: 题型:解答题
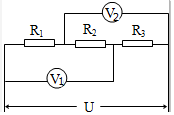 如图所示电路中定值电阻R1=5Ω,R3=20Ω,把它们与R2串联后接在电压为U的稳压电源上时.电压表V1的示数为10V,V2示数为25V,则R2的阻值和电源电压U的值分别为多少?
如图所示电路中定值电阻R1=5Ω,R3=20Ω,把它们与R2串联后接在电压为U的稳压电源上时.电压表V1的示数为10V,V2示数为25V,则R2的阻值和电源电压U的值分别为多少?查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
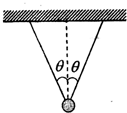 如图所示,两条等长的细绳的一端固定于水平横梁的两点,另一端悬吊一重物,绳与竖直方向的夹角θ可取不同的值,此时绳的张力为F1.如图,突然剪断其中一根绳,则在剪断瞬间,另一根绳的张力为F2,比较F1和F2的大小,我们作出的判定是F2>F1.
如图所示,两条等长的细绳的一端固定于水平横梁的两点,另一端悬吊一重物,绳与竖直方向的夹角θ可取不同的值,此时绳的张力为F1.如图,突然剪断其中一根绳,则在剪断瞬间,另一根绳的张力为F2,比较F1和F2的大小,我们作出的判定是F2>F1.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图是一种腹部先着水的跳水比赛,击水时水花最大者获胜,水花的大小主要取决于运动员入水时具有的动能.假设甲、乙运动员都站在3m高的平台上(甲、乙站立时的重心位置离平台均为1m),其中质量为120kg的甲简单的步出平台倒向水面,若质量为100kg的乙要想不输于甲,则需通过起跳使自身重心至少升高约( )
如图是一种腹部先着水的跳水比赛,击水时水花最大者获胜,水花的大小主要取决于运动员入水时具有的动能.假设甲、乙运动员都站在3m高的平台上(甲、乙站立时的重心位置离平台均为1m),其中质量为120kg的甲简单的步出平台倒向水面,若质量为100kg的乙要想不输于甲,则需通过起跳使自身重心至少升高约( )| A. | 0.6m | B. | 0.8m | C. | 1.6m | D. | 1.8m |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,A、B两条直线是在A.B两地分别用竖直向上的力F拉质量分别为mA和
如图所示,A、B两条直线是在A.B两地分别用竖直向上的力F拉质量分别为mA和| A. | mA<mB | B. | 两地重力加速度gA>gB | ||
| C. | mA>mB | D. | 两地重力加速度gA=gB |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,一对很大的直放置的平行板电容器与一分压电路相连,之间形成一水平匀强电场,其中两板间距离为d.有一轻质细绳处于电场中,绳OA可绕 0点无摩擦转动,其末端4处固定一带电量-q、质量为m的小球,绳静止在与竖直方向成37°角的位置(重力加速度为g,sin 37°=0.6,COS37°=0.8 ).试求:
如图所示,一对很大的直放置的平行板电容器与一分压电路相连,之间形成一水平匀强电场,其中两板间距离为d.有一轻质细绳处于电场中,绳OA可绕 0点无摩擦转动,其末端4处固定一带电量-q、质量为m的小球,绳静止在与竖直方向成37°角的位置(重力加速度为g,sin 37°=0.6,COS37°=0.8 ).试求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com