
 s电动机达到额定功率,此后电动机功率保持不变,金属棒运动的v—t图象如图丙所示。试求磁感应强度B1的大小和小电动机刚达到额定功率时金属棒的速度v1的大小?
s电动机达到额定功率,此后电动机功率保持不变,金属棒运动的v—t图象如图丙所示。试求磁感应强度B1的大小和小电动机刚达到额定功率时金属棒的速度v1的大小?  |



 -mgsinθ-
-mgsinθ- =0
=0
 -mgsinθ-
-mgsinθ- =
= ……
……

 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:高中物理 来源:不详 题型:问答题


查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
 r/s的转速匀速转动,线圈通过滑环和电刷与R=9Ω的电阻组成闭合回路(电压表是交流电表),求:
r/s的转速匀速转动,线圈通过滑环和电刷与R=9Ω的电阻组成闭合回路(电压表是交流电表),求:
 的表达式;
的表达式; =
= ,安培力的力矩 M安=?
,安培力的力矩 M安=? =?
=?查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题

查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
 。磁场的磁感强度为B,方向垂直纸面向里。现有一段长度为
。磁场的磁感强度为B,方向垂直纸面向里。现有一段长度为 、电阻为
、电阻为 的均匀导体杆MN架在导线框上,开始时紧靠ac,然后沿ab方向以恒定速度v向b端滑动,滑动中始终与ac平行并与导线框保持良好接触。当MN滑过的距离为
的均匀导体杆MN架在导线框上,开始时紧靠ac,然后沿ab方向以恒定速度v向b端滑动,滑动中始终与ac平行并与导线框保持良好接触。当MN滑过的距离为 时,导线ac中的电流是多大?方向如何?
时,导线ac中的电流是多大?方向如何?
查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题

查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
 。将发电机的输出端接入图中的装置K后,装置K能使交流电变成直流电,而不改变其电压的大小。直流电的另一个输出端与一可变电阻R相连,可变电阻的另一端P是直流电的正极,直流电的另一个输出端Q是它的负极。
。将发电机的输出端接入图中的装置K后,装置K能使交流电变成直流电,而不改变其电压的大小。直流电的另一个输出端与一可变电阻R相连,可变电阻的另一端P是直流电的正极,直流电的另一个输出端Q是它的负极。
查看答案和解析>>
科目:高中物理 来源:不详 题型:实验题

查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
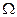 的定值电阻,在距左端
的定值电阻,在距左端 =2m处垂直导轨放置一根质量m=1kg、电阻r=0.5
=2m处垂直导轨放置一根质量m=1kg、电阻r=0.5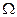 的导体棒,导体棒与导轨始终保持良好接触,导轨的电阻可忽略,整个装置处在竖直向上的匀强磁场中。
的导体棒,导体棒与导轨始终保持良好接触,导轨的电阻可忽略,整个装置处在竖直向上的匀强磁场中。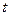 变化的关系为
变化的关系为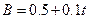 (式中B的单位为T,
(式中B的单位为T,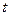 的单位为s),为使导体棒保持静止,求作用在导体棒上的水平拉力F随时间
的单位为s),为使导体棒保持静止,求作用在导体棒上的水平拉力F随时间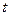 变化的规律;
变化的规律; T恒定,
T恒定, 时导体棒在水平拉力F的作用下从静止开始向右做匀加速直线运动,已知
时导体棒在水平拉力F的作用下从静止开始向右做匀加速直线运动,已知 s时F=3N,求此时导体棒两端的电势差。
s时F=3N,求此时导体棒两端的电势差。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com