
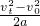
 =45m
=45m 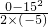 m=22.5m
m=22.5m 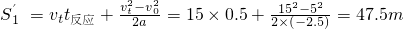
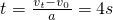
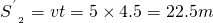
 =2ax,分别求出超载和不超载时前进的位移
=2ax,分别求出超载和不超载时前进的位移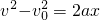 ,结合具体的位移关系判断追及问题,不很麻烦,但要注意统一用国际单位制
,结合具体的位移关系判断追及问题,不很麻烦,但要注意统一用国际单位制 

 快捷英语周周练系列答案
快捷英语周周练系列答案科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
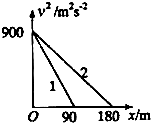 随着机动车数量的增加,交通安全问题日益凸显,分析交通违法事例,将警示我们遵守交通法规,珍惜生命.如图所示为某型号车紧急制动时(假设做匀减速直线运动)的v2-x图象(v为货车的速度,x为制动距离),其中图线1为满载时的制动图象,图线2为严重超载时的制动图象.某路段限速72km/h,是根据该型号货车满载时由安全制动时间和制动距离确定的,现有一辆该型号的货车严重超载并以54km/h的速度行驶.通过计算求解:
随着机动车数量的增加,交通安全问题日益凸显,分析交通违法事例,将警示我们遵守交通法规,珍惜生命.如图所示为某型号车紧急制动时(假设做匀减速直线运动)的v2-x图象(v为货车的速度,x为制动距离),其中图线1为满载时的制动图象,图线2为严重超载时的制动图象.某路段限速72km/h,是根据该型号货车满载时由安全制动时间和制动距离确定的,现有一辆该型号的货车严重超载并以54km/h的速度行驶.通过计算求解:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com