两个人要将质量M=1000Kg的小车沿一小型铁轨推上长L=5m,高h=1m的斜坡顶端,已知车在任何情况下所受的摩擦阻力恒为车重的0.12倍,两人能发挥的最大推力各为F=800N,在不允许使用别的工具的情况下,两人能否将车刚好推到坡顶?若能,应如何办?(g=10m/s2)
解:两个人的最大推力为F
m=2F=1600N
货物所受摩擦力始终为F
f=0.12G=1200N.
又重力沿斜面向下的分力为
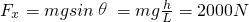
.
由于F
m<F
f+F
x,故两人不可能直接将货物推上斜面.
注意到F
m>F
f,我们可以让货物先在水平面上作匀加速运动,使货物在滑上斜面之前已经获得速度,然后匀减速滑动斜面顶端.
设货物在水平面上作匀加速直线运动的距离为s,在此运动过程中,由牛顿第二定律得F
m-f=ma
1,则货物在水平面上作加速运动所获得的速度为
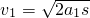
.
货物滑上斜面后作匀减速运动,设其加速度大小为a
2,则由牛顿第二定律得F
x+f-F
m=ma
2,其中F
x为货物重力的下滑分力,

要使货物恰好能滑到顶端,则有v=
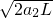
.
所以,货物在水平面上加速的距离应为s=
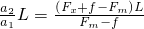
代入数据解得s=20m.
故可设计方案为:两人用最大推力使货物在水平面上至少滑行20m后再推物体滑上斜面.
分析:通过对货物进行受力分析,比较两个推力与摩擦力和重力沿斜面方向分力之和的大小,判断能否将货物推进车厢.
可以先让货物在水平面上做匀加速直线运动,以一定的初速度滑上木板,初速度越大,越容易滑进车厢,运用牛顿第二定律,结合运动学公式求出货物刚好滑进车厢时在水平面上加速的距离.
点评:解决本题的关键能够正确进行受力分析,运用牛顿第二定律结合运动学公式进行求解.

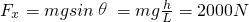 .
.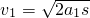 .
.
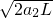 .
.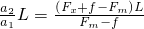


 名校课堂系列答案
名校课堂系列答案