
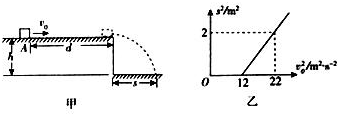
���� ��1�����о������A����ƽ̨��Ե�Ĺ��̣��ɶ��ܶ�����û��鵽��ƽ̨��Եʱ���ٶȣ������뿪ƽ̨����ƽ���˶����ٸ���ƽ���˶��Ĺ��ɵõ�s2��v02�Ĺ�ϵʽ������ͼ������壬��⼴�ɣ�
��2�����������̣����ö��ܶ�������黬��ƽ̨�����ʱ���ٶ�v�䣮�ɶ��ܶ���������鵽��ƽ̨��Եʱ���ٶȣ����ƽ���˶��Ĺ�����ˮƽ���룮
��� �⣺��1���軬�黬��ƽ̨��Եʱ���ٶ�Ϊv�����ݶ��ܶ����ã�
-��mgd=$\frac{1}{2}m{v}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$����
�����뿪ƽ̨����ƽ���˶������У�
h=$\frac{1}{2}g{t}^{2}$����
s=vt����
����������ʽ�ã�s2=$\frac{2h}{g}$v02-4��hd����
��ͼ��ã�ͼ���б�ʵ���$\frac{2h}{g}$������$\frac{2h}{g}$=$\frac{2}{22-12}$=0.2����
��ã�h=1m
�ҵ�s=0��${v}_{0}^{2}$=12��������ʽ�ܽ�ã�d=2m
��2���ɢٵã�v=2m/s
�����뿪ƽ̨����ƽ���˶������У�h=$\frac{1}{2}g{t}^{2}$����
�ã�t=$\sqrt{\frac{2h}{g}}$=$\sqrt{\frac{2��1}{10}}$=$\frac{\sqrt{5}}{5}$s����
��黬��ƽ̨�����ʱ���ٶ�Ϊ��v��=$\sqrt{{v}^{2}+��gt��^{2}}$=2$\sqrt{6}$m/s
��ص���ƽ̨��ˮƽ����s�Ĵ�СΪ��s=vt=2��$\frac{\sqrt{5}}{5}$m=$\frac{2\sqrt{5}}{5}$m
�𣺣�1��ƽ̨��صĸ߶�h��1m��������ƽ̨�ϻ��еľ���dΪ2m��
��2����黬��ƽ̨�����ʱ���ٶ�v����2$\sqrt{6}$m/s����ص���ƽ̨��ˮƽ����s�Ĵ�С��$\frac{2\sqrt{5}}{5}$m��
���� �����Ƕ��ܶ�������ƽ���˶����ۺ�Ӧ�ã��ؼ�Ҫ����������˶����̣�����ÿ�����̵��������ɣ����ö��ܶ������˶�ѧ��ʽ�����о���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
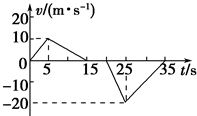 ����m=50kg��ijͬѧվ�ڹ۹���ݵذ��ϣ����ٶȴ�������¼�˵�����һ��ʱ�����˶����ٶ���ʱ��仯���������ֱ����Ϊ��������ͼ���ṩ����Ϣ��֪��������
����m=50kg��ijͬѧվ�ڹ۹���ݵذ��ϣ����ٶȴ�������¼�˵�����һ��ʱ�����˶����ٶ���ʱ��仯���������ֱ����Ϊ��������ͼ���ṩ����Ϣ��֪��������| A�� | ��0��15s�ڣ��۹���������ĸ߶�Ϊ25m | |
| B�� | ��0��35s�ڣ��۹���ݵ�ƽ������Ϊ6m/s | |
| C�� | ��20��25s��25��35 s�ڣ��۹���ݵ�ƽ���ٶȴ�С��Ϊ10m/s | |
| D�� | ��25��35s�ڣ��۹�����ڼ�����������ͬѧ�ļ��ٶȴ�СΪ2m/s2 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ����ΪL��ϸ��һ�˹̶�����һ��ϵһ����Ϊm��С��С������ֱƽ���ڰڶ���ͨ����͵�ʱ���ٶ�Ϊv�����ʱϸ�߶�С�������Ĵ�СΪ��������
��ͼ��ʾ����ΪL��ϸ��һ�˹̶�����һ��ϵһ����Ϊm��С��С������ֱƽ���ڰڶ���ͨ����͵�ʱ���ٶ�Ϊv�����ʱϸ�߶�С�������Ĵ�СΪ��������| A�� | mg | B�� | m$\frac{v^2}{L}$ | C�� | mg+m$\frac{v^2}{L}$ | D�� | mg-m$\frac{v^2}{L}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | v=k$\frac{P}{��}$ | B�� | v=$\sqrt{\frac{kP}{��}}$ | C�� | v=$\sqrt{\frac{k��}{P}}$ | D�� | v=$\sqrt{kP��}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
 ������ȤС��Ҫ����һ�綯����صĵ綯�ƺ����裮��֪�õ�ص綯��Ϊ10��12V��ʵ���ұ����������ģ�
������ȤС��Ҫ����һ�綯����صĵ綯�ƺ����裮��֪�õ�ص綯��Ϊ10��12V��ʵ���ұ����������ģ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��˹�ط����˵����Ĵ�ЧӦ | B�� | ����Ԥ�Թ�Ҳ�ǵ�Ų� | ||
| C�� | �����ڷ����˵�Ÿ�Ӧ���� | D�� | �����״η�����X���� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com