
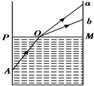
 如图所示,容器中盛有水,PM为水面,从A点发出一束白光,射到水面上的O点后,折射光(发生了色散)照到器壁上a、b之间,如果AP=OM=$\sqrt{3}$ m,PO=Mb=1m,ab=($\sqrt{3}$-1)m,则从A点发出的白光射到PM上的入射点O向右移动多少时开始有色光消失?移动多少时器壁上的色光全部消失?
如图所示,容器中盛有水,PM为水面,从A点发出一束白光,射到水面上的O点后,折射光(发生了色散)照到器壁上a、b之间,如果AP=OM=$\sqrt{3}$ m,PO=Mb=1m,ab=($\sqrt{3}$-1)m,则从A点发出的白光射到PM上的入射点O向右移动多少时开始有色光消失?移动多少时器壁上的色光全部消失? 分析 由于三棱镜对各色光的折射率不同,导致色散的形成.根据几何关系求出两种色光在O点的入射角和折射角,由折射定律求出折射率,再由sinC=$\frac{1}{n}$求出临界角.结合全反射条件和几何关系求解.
解答 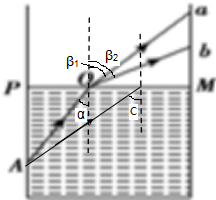 解:设水对射到a点的光线折射率为n1,全反射临界角为C1.水对射到b点的光线折射率为n2,全反射临界角为C2.光路图如图.
解:设水对射到a点的光线折射率为n1,全反射临界角为C1.水对射到b点的光线折射率为n2,全反射临界角为C2.光路图如图.
由几何关系可得:
tanα=$\frac{PO}{AP}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,得 α=30°
tanβ1=$\frac{OM}{Ma}$=$\frac{\sqrt{3}}{\sqrt{3}}$=1,得 β1=45°
tanβ2=$\frac{OM}{Mb}$=$\frac{\sqrt{3}}{1}$=$\sqrt{3}$,得 β2=60°
由折射定律得:n1=$\frac{sin{β}_{1}}{sinα}$=$\sqrt{2}$,n2=$\frac{sin{β}_{2}}{sinα}$=$\sqrt{3}$
由sinC=$\frac{1}{n}$得:sinC1=$\frac{\sqrt{2}}{2}$,C1=45°;sinC2=$\frac{\sqrt{3}}{3}$,cosC2=$\sqrt{1-si{n}^{2}{C}_{2}}$=$\frac{\sqrt{6}}{3}$
当从A点发出的白光射到PM上的入射点O向右移动时,折射率为n2的光线先发生全反射,O点向右移动的距离为
S1=APtanC2-PO=AP$\frac{sin{C}_{2}}{cos{C}_{2}}$-PO=$\sqrt{3}$×$\frac{\frac{\sqrt{3}}{3}}{\frac{\sqrt{6}}{3}}$-1=$\frac{\sqrt{6}-1}{2}$m
当从A点发出的白光射到PM上的入射点O向右移动时,折射率为n1的光线先发生全反射,O点向右移动的距离为
S2=APtanC1-PO=AP-PO=($\sqrt{3}$-1)m
即移动($\sqrt{3}$-1)m时器壁上的色光全部消失.
答:从A点发出的白光射到PM上的入射点O向右移动$\frac{\sqrt{6}-1}{2}$m时开始有色光消失,移动($\sqrt{3}$-1)m时器壁上的色光全部消失.
点评 本题是光的色散现象,可以用红光与紫光类比,根据紫光的折射率最大,红光的折射率最小进行类比分析,就比较容易理解了.


 应用题作业本系列答案
应用题作业本系列答案科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 在t=1s时,滑块的加速度为零 | |
| B. | 在4~6s时间内,滑块的平均速度为3 m/s | |
| C. | 在3~7s时间内,合力做功的平均功率为2 W | |
| D. | 在5~6s时间内,滑块受到的合力大小为2 N |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
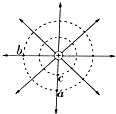 真空中点电荷的电场如图所示,则a点和b点电场强度不相同(选填“相同”或“不相同”);a点的电势低于(选填“高于”、“等于”或“低于”)c点电势.
真空中点电荷的电场如图所示,则a点和b点电场强度不相同(选填“相同”或“不相同”);a点的电势低于(选填“高于”、“等于”或“低于”)c点电势.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 研究地球自转时,地球可以看作质点 | |
| B. | 研究月球绕地球运行的时间时,可将月球视为质点 | |
| C. | 研究乒乓球的弧圈运动时,可将乒乓球视为质点 | |
| D. | 因原子核很小,所以在研究原子核结构时,可把原子核看作质点 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
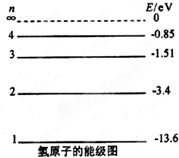
| A. | 一群原处于n=4能级的氢原子回到n=1的状态过程中,最多放出6种频率不同的光子 | |
| B. | 一群原处于n=4能级的氢原子回到n=1的状态过程中,最多放出3种频率不同的光子 | |
| C. | 一个原处于n=4能级的氢原子回到n=1的状态过程中,最多放出6种频率不同的光子 | |
| D. | 一个原处于n=4能级的氢原子回到n=1的状态过程中,最多放出3种频率不同的光子 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
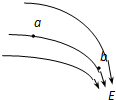 如图所示是电场中某区域的电场线,a、b两点的电场强度大小关系为Ea<Eb,同一试探电荷放在a、b两点所受到的电场力大小关系为Fa<Fb(选填“>”“<”或“=”)
如图所示是电场中某区域的电场线,a、b两点的电场强度大小关系为Ea<Eb,同一试探电荷放在a、b两点所受到的电场力大小关系为Fa<Fb(选填“>”“<”或“=”)查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com