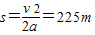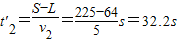Question

甲车以15m/s的速度在平直公路上匀速行驶，突然发现26m处乙车正以10m/s的速度做同方向的匀速直线运动．甲车立即关闭油门并以大小为0.5m/s²的加速度做匀减速直线运动，则
（1）甲车能撞上自行车吗？若不能相撞，两车最小距离是多少？
（2）若乙的速度是5m/s，且甲乙在平行的两条路上，相距64m，其余同上．则甲乙能相遇几次？各是什么时刻相遇？

Answer 1

【答案】分析：两车是否相撞关键点是：两着速度相等时若没有相撞，后面的时间里，后面的汽车速度下，前面的自行车速度大，以后永不相撞．
解答：解：（1）设两车从0时刻至速度相同的时间为t
则有v_t=v+at=15+（-0.5）×t=10
解得：t=10s
10秒内甲车位移为：
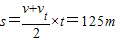
乙车的位移：s=10×10=100m
两车距离缩短了125-100=25m，本来距离26m，所以无法相撞．  
速度相等时两车距离最小是4-3=1m．                           
（2）当两车速度相等时，时间为t，
根据：v=v+at得 t=20s
该段时间内，甲车位移S₁=200m，
乙车位移S₂=100m
甲比乙多走△S=S₁-S₂=100m＞64m，所以肯定会相遇两次．        
设经过时间t两车相遇，初始相距L=64m，
则
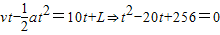
解出的t₁=8s  t₂=32s                                    
因为甲车减速到零的时间，
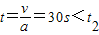
所以第二次相遇应该是乙车匀速运动到甲车停止处的时间，
设为t′₂，
甲车减速到零的位移为s，
据v²-v²=2as
得
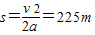
所以
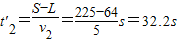
故两车相遇两次，分别在t₁=8s和t′₂=32.2s相遇．
答：（1）甲车不能撞上自行车；若不能相撞，两车最小距离是1m；
（2）若乙的速度是5m/s，且甲乙在平行的两条路上，相距64m，其余同上．则甲乙能相遇两次；分别在t₁=8s和t′₂=32.2s相遇．
点评：追及问题解题关键思路：①两个关系：时间关系和位移关系②一个条件：两者速度相等，是能否追上的关键．
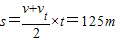
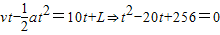
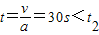