骑自行车的人以6m/s的初速度匀减速地骑上一个斜坡.已知加速度的大小为0.4m/s2,,斜坡长40m.问:
(1)骑自行车的人通过斜坡要用多长时间?
(2)自行车骑上斜坡坡顶的速度为多少?
(3)第3s内通过的距离是多少?
【答案】
分析:(1)骑自行车的人做匀减速直线运动,已知初速度、加速度和位移,根据位移公式求出时间.
(2)根据速度公式求出自行车骑上斜坡坡顶的速度.
(3)第3s内通过的距离等于前3s内与前2s位移之差.由位移公式求解.
解答:解:已知初速度v
=6m/s、加速度a=-0.4m/s
2,位移x=40m.
(1)由x=v
t+

得,
40=6t-

t
2解得,t
1=10s,t
2=20s
由于骑自行车的人做匀减速直线运动,经过t=
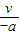
=15s停止运动,所以t
2=20s不合理,舍去.
(2)自行车骑上斜坡坡顶的速度为v=v
+at=2m/s
(3)前3s内的位移为x
3=v
t
3+
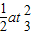
=16.2m
前2s位移为x
2=v
t
2+
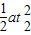
=11.2m.
所以第3s内通过的距离是S=x
3-x
2=5m.
答:
(1)骑自行车的人通过斜坡要用10s时间.
(2)自行车骑上斜坡坡顶的速度为2m/s.
(3)第3s内通过的距离是5m.
点评:本题是匀减速直线运动问题,要注意加速度是负值,并要检验解题结果是否合理.基础题.

 得,
得, t2
t2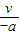 =15s停止运动,所以t2=20s不合理,舍去.
=15s停止运动,所以t2=20s不合理,舍去.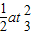 =16.2m
=16.2m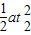 =11.2m.
=11.2m.
