

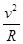 ,细线拉力为零,对支架受力分析,支架受重力和地面对它的支持力,处于静止状态.所以在释放瞬间,支架对地面压力为Mg.故A错误.
,细线拉力为零,对支架受力分析,支架受重力和地面对它的支持力,处于静止状态.所以在释放瞬间,支架对地面压力为Mg.故A错误.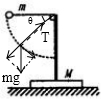
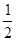 mv2,v=
mv2,v=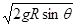 ,根据牛顿第二定律得:T-mgsinθ=m
,根据牛顿第二定律得:T-mgsinθ=m

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中物理 来源: 题型:
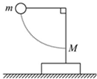 如图所示,放置在水平地面上的支架质量为M,支架顶端用细线拴着的摆球质量为m,现将摆球拉至水平位置,而后释放,摆球运动过程中,支架始终不动,以下说法正确的是
如图所示,放置在水平地面上的支架质量为M,支架顶端用细线拴着的摆球质量为m,现将摆球拉至水平位置,而后释放,摆球运动过程中,支架始终不动,以下说法正确的是| A、在释放前的瞬间,支架对地面的压力为(m+M)g | B、在释放前的瞬间,支架对地面的压力为mg | C、摆球到达最低点时,支架对地面的压力为(m+M)g | D、摆球到达最低点时,支架对地面的压力为(3m+M)g |
查看答案和解析>>
科目:高中物理 来源: 题型:
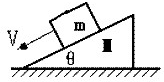 如图所示,放置在水平地面上的直角劈M上有一个质量为m的物体,若m在直角劈上面匀加速下滑,M仍保持静止,那么正确的说法是( )
如图所示,放置在水平地面上的直角劈M上有一个质量为m的物体,若m在直角劈上面匀加速下滑,M仍保持静止,那么正确的说法是( )| A、M对地面的压力等于(M+m)g | B、M对地面的压力大于(M+m)g | C、地面对M没有摩擦力 | D、地面对M有向左的摩擦力 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com