
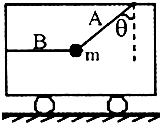
 如图所示,在水平地面的车厢中,一小球被两根轻质细绳A、B栓住,其中A与竖直方向成θ角,B成水平状态,小球的质量为m,重力加速度为g,求:
如图所示,在水平地面的车厢中,一小球被两根轻质细绳A、B栓住,其中A与竖直方向成θ角,B成水平状态,小球的质量为m,重力加速度为g,求: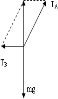
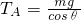 ,TB=mgtanθ.
,TB=mgtanθ.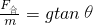 .
.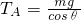 ,TB=ma2+mgtanθ.
,TB=ma2+mgtanθ.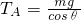 ,TB=mgtanθ.
,TB=mgtanθ.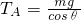 ,TB=ma2+mgtanθ.
,TB=ma2+mgtanθ.

科目:高中物理 来源: 题型:
 (2010?宝山区一模)如图所示,在水平地面附近小球B以初速度v斜向上瞄准另一小球A射出,恰巧在B球射出的同时,A球由静止开始下落,不计空气阻力.则两球在空中运动的过程中( )
(2010?宝山区一模)如图所示,在水平地面附近小球B以初速度v斜向上瞄准另一小球A射出,恰巧在B球射出的同时,A球由静止开始下落,不计空气阻力.则两球在空中运动的过程中( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,在水平地面MN上方空间存在一垂直纸面向里、磁感应强度B=1T的有界匀强磁场区域,上边界EF距离地面的高度为H.正方形金属线框abcd的质量m=0.02kg、边长L=0.1m(L<H),总电阻R=0.2Ω,开始时线框在磁场上方,ab边距离EF高度为h,然后由静止开始自由下落,abcd始终在竖直平面内且ab保持水平.线框从开始运动到ab边刚要落地的过程中(g取10m/s2):
如图所示,在水平地面MN上方空间存在一垂直纸面向里、磁感应强度B=1T的有界匀强磁场区域,上边界EF距离地面的高度为H.正方形金属线框abcd的质量m=0.02kg、边长L=0.1m(L<H),总电阻R=0.2Ω,开始时线框在磁场上方,ab边距离EF高度为h,然后由静止开始自由下落,abcd始终在竖直平面内且ab保持水平.线框从开始运动到ab边刚要落地的过程中(g取10m/s2):查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,在水平地面MN上方有一个粗糙绝缘平台PQ,高度为h=1m平台上方PR右侧有水平向右的有界匀强电场,PR左侧有竖直向上的匀强电场,场强大小均为E=1.1×l04N/C有一质量m=1.0×10-3kg、电荷量为q=-2.0×10-6C的滑块,放在距离平台左端P点L=1.2m处,滑块与平台间的动摩擦因数u=0.2,现给滑块水平向左的初速度v0=4m/s,取g=10m/s2,求:
如图所示,在水平地面MN上方有一个粗糙绝缘平台PQ,高度为h=1m平台上方PR右侧有水平向右的有界匀强电场,PR左侧有竖直向上的匀强电场,场强大小均为E=1.1×l04N/C有一质量m=1.0×10-3kg、电荷量为q=-2.0×10-6C的滑块,放在距离平台左端P点L=1.2m处,滑块与平台间的动摩擦因数u=0.2,现给滑块水平向左的初速度v0=4m/s,取g=10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:
 (2009?日照一模)如图所示,在水平地面下埋着一条沿东西方向通有恒定电流的水平直导线.现用一串有灵敏电流计的闭合圆形检测线圈检测此通电直导线的位置.若不考虑地磁场的影响,检测线圈在水平面内,从距直导线很远处的北边移至距直导线很远处的南边的过程中,俯视检测线圈.下列说法正确的是( )
(2009?日照一模)如图所示,在水平地面下埋着一条沿东西方向通有恒定电流的水平直导线.现用一串有灵敏电流计的闭合圆形检测线圈检测此通电直导线的位置.若不考虑地磁场的影响,检测线圈在水平面内,从距直导线很远处的北边移至距直导线很远处的南边的过程中,俯视检测线圈.下列说法正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,在水平地面下有一条沿东西方向铺设的水平直导线,导线中通有自东向西稳定、强度较大的直流电流.现用一闭合的检测线圈(线圈中串有灵敏电流计,图中未画出)检测此通电直导线的位置,若不考虑地磁场的影响,在检测线圈位于水平面内,从距直导线很远处由北向南沿水平地面通过导线的上方并移至距直导线很远处的过程中,俯视检测线圈,其中的感应电流的方向是:( )
如图所示,在水平地面下有一条沿东西方向铺设的水平直导线,导线中通有自东向西稳定、强度较大的直流电流.现用一闭合的检测线圈(线圈中串有灵敏电流计,图中未画出)检测此通电直导线的位置,若不考虑地磁场的影响,在检测线圈位于水平面内,从距直导线很远处由北向南沿水平地面通过导线的上方并移至距直导线很远处的过程中,俯视检测线圈,其中的感应电流的方向是:( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com