
| A�� | �����������ٶ��ǵ�һ�����ٶȵ�$\frac{1}{n}$�� | |
| B�� | �����ǵ������ٶ��ǵ������������������ת��õ��ٶȵ�$\frac{1}{n}$�� | |
| C�� | �����������ٶ��ǵ�һ�����ٶ�$\sqrt{\frac{1}{n}}$�� | |
| D�� | �����ǵ����ļ��ٶ��ǵ�������������ٶȵ�$\frac{1}{{n}^{2}}$�� |
���� �о�������������Ƶ���������Բ���˶����������������ṩ���������г���ʽ��ʾ����Ҫ�Ƚϵ���������
������֪����Ϲ�ϵʽ���δ֪����
��� �⣺A���о�������������Ƶ���������Բ���˶���
�������������ṩ���������г���ʽ��$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$
��ã�v=$\sqrt{\frac{GM}{r}}$������rΪ����������ǵĹ���뾶��
����������ǵĹ���뾶�ǵ���뾶��n������r=nR������v=$\sqrt{\frac{GM}{r}}$=$\sqrt{\frac{GM}{nR}}$
����һ�����ٶ�Ϊ��$\sqrt{\frac{GM}{R}}$
��������������ǵ������ٶ��ǵ�һ�����ٵ�$\sqrt{\frac{1}{n}}$������A����C��ȷ��
B������������ǵ������������ת���ڹ�ϵ��ȷ���������Ƚ����ߵ��ٶȴ�С����B����
D���о������Ƶ���������Բ���˶����������������ṩ���������г���ʽ��$\frac{GMm}{{r}^{2}}$=ma��
��ã�a=$\frac{GM}{{r}^{2}}$
���ݵ�����������������������ã�$\frac{GMm}{{R}^{2}}$=mg��
��ã�g=$\frac{GM}{{R}^{2}}$
$\frac{a}{g}$=$\frac{{R}^{2}}{{r}^{2}}$=$\frac{1}{{n}^{2}}$
����ͬ�����ǵ����ļ��ٶ��ǵ�������������ٶȵ�$\frac{1}{{n}^{2}}$������D��ȷ��
��ѡ��CD��
���� ��һ��������֮�ȣ�����Ӧ�ð����������������֪����������ʾ�������ٸ��ݱ���ʽ���бȽϣ�
�������Ĺ�ʽѡȡҪ������Ŀ�ṩ����֪��������������������ѡȡӦ�ã�


 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��

| A�� | ��A����B | B�� | ��A=��B | C�� | vA��vB | D�� | vA��vB |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 �������о�ƽ��������˶�����ʵ��ʱ��
�������о�ƽ��������˶�����ʵ��ʱ���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���Ǿ������ĸ߶�Ϊ$\root{3}{\frac{GM{T}^{2}}{4{��}^{2}}}$-R | |
| B�� | �����ǵķ����ٶ�ӦС��11.2km/s | |
| C�� | ��������ʱ�ܵ�����������СΪG$\frac{Mm}{{R}^{2}}$ | |
| D�� | �������е����ļ��ٶ�С�ڵ��������������ٶ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ����ˮƽ�������ȱ���ֱ���˶��ij����У�������С�������ƫ����ֱ����37��ǣ���ͳ�����Ծ�ֹ���������Ϊ1kg����g=10m/s2��sin37��=0.6��cos37��=0.8��
��ͼ��ʾ����ˮƽ�������ȱ���ֱ���˶��ij����У�������С�������ƫ����ֱ����37��ǣ���ͳ�����Ծ�ֹ���������Ϊ1kg����g=10m/s2��sin37��=0.6��cos37��=0.8���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 �ڹ�·�ϳ��ῴ���κͰ��ε�·�棬��ͼ��ʾ��һ����Ϊm��������ͨ����·�����ߴ�ʱ��·���ѹ��ΪN1��ͨ������·����ʹ�ʱ��·���ѹ��ΪN2��������
�ڹ�·�ϳ��ῴ���κͰ��ε�·�棬��ͼ��ʾ��һ����Ϊm��������ͨ����·�����ߴ�ʱ��·���ѹ��ΪN1��ͨ������·����ʹ�ʱ��·���ѹ��ΪN2��������| A�� | N1��mg | B�� | N1��mg | C�� | N2��N1 | D�� | N2��N1 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
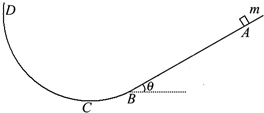 ��ͼ��ʾ����Ǧ�=37���б����⻬Բ��$\widehat{BCD}$������B�㣬����װ�ù̶�����ֱƽ���ڣ���һ����m=2.0kg����Ϊ�ʵ�����壬��б���ϵ�A����ֹ�»���AB��L=3.0m��������б���Ķ�Ħ��������=0.5�����ƿ���������ȡ�������ٶ�g=10m/s2��sin37��=0.6��cos37��=0.8����
��ͼ��ʾ����Ǧ�=37���б����⻬Բ��$\widehat{BCD}$������B�㣬����װ�ù̶�����ֱƽ���ڣ���һ����m=2.0kg����Ϊ�ʵ�����壬��б���ϵ�A����ֹ�»���AB��L=3.0m��������б���Ķ�Ħ��������=0.5�����ƿ���������ȡ�������ٶ�g=10m/s2��sin37��=0.6��cos37��=0.8�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �ɺ�·�̱�� | B�� | �ɺ�ʱ�䲻�� | ||
| C�� | �����ʱ���ٶ����� | D�� | �ɺ�ͨ����·�̱�λ��Ҫ�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com