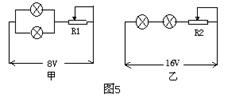
如图5所示，把两个相同的灯泡分别接在甲、乙电路中，甲电路两端的电压为8V，乙电路两端的电压为16V。调节变阻器R1和R2使两灯都正常发光，此时变阻器消耗的功率分别为P1和P2，两电路中消耗的总功率分别为P甲和P乙则下列关系中正确的是（ ）
A．P甲＜P乙 B．P甲＞P乙
C． P1＞P2 D． P1＝P2
开心练习课课练与单元检测系列答案科目：高中物理 来源： 题型：阅读理解
查看答案和解析>>
科目：高中物理 来源： 题型：阅读理解
| m(s1+s2)2f2 |
| 32 |
| m(s1+s2)2f2 |
| 32 |
| (s2-s1)f2 |
| 4 |
| (s2-s1)f2 |
| 4 |
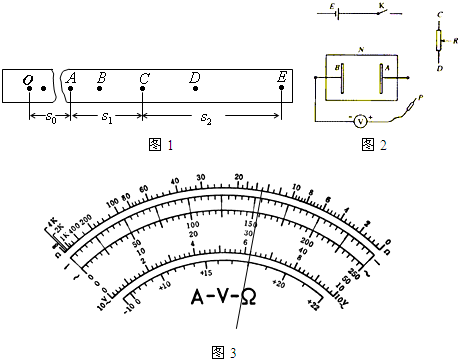
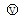（量程为6V，内阻很大，其负接线柱与B极相连，正接线柱与探针P相连），开关K．现要用图中仪器描绘两平行金属条AB间电场中的等势线．AB间的电压要求取为6V．查看答案和解析>>
科目：高中物理 来源： 题型：
A．为完成电场中等势线的描绘实验，某同学准备使用如图16所示的实验器材：查看答案和解析>>
科目：高中物理 来源： 题型：阅读理解
（1）在寻找黑匣子的过程中，测量船在其上方湖面向湖底发射波速为1 450 m/s的超声波，并测得各超声波从发射到返回湖面经历了0.2 s，则黑匣子所在湖域的深度约为_______m.
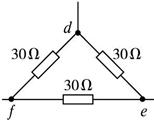
图1
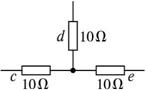
图2 图3
（2）出水后，技术人员要对黑匣子中的电路的导通情况进行检测，图1是黑匣子某部分电路图，图中R1标有“5 V2.5 W”字样，滑动变阻器R2标有“5 Ω1 A”字样，电流表量程采用0—0.6 A，电压表量程采用0—3 V.
①若该电路各元件均完好，为了检测过程中的任何时候确保电路各部分安全，在a、b间所加电源电压的最大值应为__________V；
②如果测定时电压表示数U如图2所示，则U=__________V.
（3）另一部分电路装在一个小盒子里，盒子内部是由三个电阻连接而成，并且盒外的三根引出线相连接，如图3所示.当把两根引出线cd接3 V恒压源时，测得其余任意两根引出线之间的电压均为1.5 V,且流过此电压源的电流为0.15 A；当将3 V恒压源接ce或de时，测得其余任意两根引出线之间的电压仍均为1.5 V,流过电压源的电流也为0.15 A.画出小盒子内部的电路结构，并标明每个电阻的阻值.
查看答案和解析>>
科目：高中物理 来源： 题型：阅读理解
第一部分 力＆物体的平衡
第一讲 力的处理
一、矢量的运算
1、加法
表达：
+ 
= 
。
名词：
为“和矢量”。
法则：平行四边形法则。如图1所示。
和矢量大小：c = 
，其中α为
和
的夹角。
和矢量方向：
在
、
之间，和
夹角β= arcsin
2、减法
表达：
= 
－
。
名词：
为“被减数矢量”，
为“减数矢量”，
为“差矢量”。
法则：三角形法则。如图2所示。将被减数矢量和减数矢量的起始端平移到一点，然后连接两时量末端，指向被减数时量的时量，即是差矢量。
差矢量大小：a = 
，其中θ为
和
的夹角。
差矢量的方向可以用正弦定理求得。
一条直线上的矢量运算是平行四边形和三角形法则的特例。
例题：已知质点做匀速率圆周运动，半径为R ，周期为T ，求它在
T内和在
T内的平均加速度大小。
解说：如图3所示，A到B点对应
T的过程，A到C点对应
T的过程。这三点的速度矢量分别设为
、
和
。
根据加速度的定义 
= 
得：
= 
，
= 
由于有两处涉及矢量减法，设两个差矢量 
= 
－
，
= 
－
，根据三角形法则，它们在图3中的大小、方向已绘出（
的“三角形”已被拉伸成一条直线）。
本题只关心各矢量的大小，显然：
= 
= 
= 
，且：
= 
= 
，
= 2
= 
所以：
= 
= 
= 
，
= 
= 
= 
。
（学生活动）观察与思考：这两个加速度是否相等，匀速率圆周运动是不是匀变速运动？
答：否；不是。
3、乘法
矢量的乘法有两种：叉乘和点乘，和代数的乘法有着质的不同。
⑴ 叉乘
表达：
×
= 
名词：
称“矢量的叉积”，它是一个新的矢量。
叉积的大小：c = absinα，其中α为
和
的夹角。意义：
的大小对应由
和
作成的平行四边形的面积。
叉积的方向：垂直
和
确定的平面，并由右手螺旋定则确定方向，如图4所示。
显然，
×
≠
×
，但有：
×
= －
×
⑵ 点乘
表达：
·
= c
名词：c称“矢量的点积”，它不再是一个矢量，而是一个标量。
点积的大小：c = abcosα，其中α为
和
的夹角。
二、共点力的合成
1、平行四边形法则与矢量表达式
2、一般平行四边形的合力与分力的求法
余弦定理（或分割成RtΔ）解合力的大小
正弦定理解方向
三、力的分解
1、按效果分解
2、按需要——正交分解
第二讲 物体的平衡
一、共点力平衡
1、特征：质心无加速度。
2、条件：Σ
= 0 ，或 
= 0 ，
= 0
例题：如图5所示，长为L 、粗细不均匀的横杆被两根轻绳水平悬挂，绳子与水平方向的夹角在图上已标示，求横杆的重心位置。
解说：直接用三力共点的知识解题，几何关系比较简单。
答案：距棒的左端L/4处。
（学生活动）思考：放在斜面上的均质长方体，按实际情况分析受力，斜面的支持力会通过长方体的重心吗？
解：将各处的支持力归纳成一个N ，则长方体受三个力（G 、f 、N）必共点，由此推知，N不可能通过长方体的重心。正确受力情形如图6所示（通常的受力图是将受力物体看成一个点，这时，N就过重心了）。
答：不会。
二、转动平衡
1、特征：物体无转动加速度。
2、条件：Σ
= 0 ，或ΣM+ =ΣM-
如果物体静止，肯定会同时满足两种平衡，因此用两种思路均可解题。
3、非共点力的合成
大小和方向：遵从一条直线矢量合成法则。
作用点：先假定一个等效作用点，然后让所有的平行力对这个作用点的和力矩为零。
第三讲 习题课
1、如图7所示，在固定的、倾角为α斜面上，有一块可以转动的夹板（β不定），夹板和斜面夹着一个质量为m的光滑均质球体，试求：β取何值时，夹板对球的弹力最小。
解说：法一，平行四边形动态处理。
对球体进行受力分析，然后对平行四边形中的矢量G和N1进行平移，使它们构成一个三角形，如图8的左图和中图所示。
由于G的大小和方向均不变，而N1的方向不可变，当β增大导致N2的方向改变时，N2的变化和N1的方向变化如图8的右图所示。
显然，随着β增大，N1单调减小，而N2的大小先减小后增大，当N2垂直N1时，N2取极小值，且N2min = Gsinα。
法二，函数法。
看图8的中间图，对这个三角形用正弦定理，有：
= 
，即：N2 = 
，β在0到180°之间取值，N2的极值讨论是很容易的。
答案：当β= 90°时，甲板的弹力最小。
2、把一个重为G的物体用一个水平推力F压在竖直的足够高的墙壁上，F随时间t的变化规律如图9所示，则在t = 0开始物体所受的摩擦力f的变化图线是图10中的哪一个？
解说：静力学旨在解决静态问题和准静态过程的问题，但本题是一个例外。物体在竖直方向的运动先加速后减速，平衡方程不再适用。如何避开牛顿第二定律，是本题授课时的难点。
静力学的知识，本题在于区分两种摩擦的不同判据。
水平方向合力为零，得：支持力N持续增大。
物体在运动时，滑动摩擦力f = μN ，必持续增大。但物体在静止后静摩擦力f′≡ G ，与N没有关系。
对运动过程加以分析，物体必有加速和减速两个过程。据物理常识，加速时，f ＜ G ，而在减速时f ＞ G 。
答案：B 。
3、如图11所示，一个重量为G的小球套在竖直放置的、半径为R的光滑大环上，另一轻质弹簧的劲度系数为k ，自由长度为L（L＜2R），一端固定在大圆环的顶点A ，另一端与小球相连。环静止平衡时位于大环上的B点。试求弹簧与竖直方向的夹角θ。
解说：平行四边形的三个矢量总是可以平移到一个三角形中去讨论，解三角形的典型思路有三种：①分割成直角三角形（或本来就是直角三角形）；②利用正、余弦定理；③利用力学矢量三角形和某空间位置三角形相似。本题旨在贯彻第三种思路。
分析小球受力→矢量平移，如图12所示，其中F表示弹簧弹力，N表示大环的支持力。
（学生活动）思考：支持力N可不可以沿图12中的反方向？（正交分解看水平方向平衡——不可以。）
容易判断，图中的灰色矢量三角形和空间位置三角形ΔAOB是相似的，所以：
⑴
由胡克定律：F = k（
- R） ⑵
几何关系：
= 2Rcosθ ⑶
解以上三式即可。
答案：arccos
。
（学生活动）思考：若将弹簧换成劲度系数k′较大的弹簧，其它条件不变，则弹簧弹力怎么变？环的支持力怎么变？
答：变小；不变。
（学生活动）反馈练习：光滑半球固定在水平面上，球心O的正上方有一定滑轮，一根轻绳跨过滑轮将一小球从图13所示的A位置开始缓慢拉至B位置。试判断：在此过程中，绳子的拉力T和球面支持力N怎样变化？
解：和上题完全相同。
答：T变小，N不变。
4、如图14所示，一个半径为R的非均质圆球，其重心不在球心O点，先将它置于水平地面上，平衡时球面上的A点和地面接触；再将它置于倾角为30°的粗糙斜面上，平衡时球面上的B点与斜面接触，已知A到B的圆心角也为30°。试求球体的重心C到球心O的距离。
解说：练习三力共点的应用。
根据在平面上的平衡，可知重心C在OA连线上。根据在斜面上的平衡，支持力、重力和静摩擦力共点，可以画出重心的具体位置。几何计算比较简单。
答案：
R 。
（学生活动）反馈练习：静摩擦足够，将长为a 、厚为b的砖块码在倾角为θ的斜面上，最多能码多少块？
解：三力共点知识应用。
答：
。
4、两根等长的细线，一端拴在同一悬点O上，另一端各系一个小球，两球的质量分别为m1和m2 ，已知两球间存在大小相等、方向相反的斥力而使两线张开一定角度，分别为45和30°，如图15所示。则m1 : m2??为多少？
解说：本题考查正弦定理、或力矩平衡解静力学问题。
对两球进行受力分析，并进行矢量平移，如图16所示。
首先注意，图16中的灰色三角形是等腰三角形，两底角相等，设为α。
而且，两球相互作用的斥力方向相反，大小相等，可用同一字母表示，设为F 。
对左边的矢量三角形用正弦定理，有：
= 
①
同理，对右边的矢量三角形，有：
= 
②
解①②两式即可。
答案：1 ：
。
（学生活动）思考：解本题是否还有其它的方法？
答：有——将模型看成用轻杆连成的两小球，而将O点看成转轴，两球的重力对O的力矩必然是平衡的。这种方法更直接、简便。
应用：若原题中绳长不等，而是l1 ：l2 = 3 ：2 ，其它条件不变，m1与m2的比值又将是多少？
解：此时用共点力平衡更加复杂（多一个正弦定理方程），而用力矩平衡则几乎和“思考”完全相同。
答：2 ：3
。
5、如图17所示，一个半径为R的均质金属球上固定着一根长为L的轻质细杆，细杆的左端用铰链与墙壁相连，球下边垫上一块木板后，细杆恰好水平，而木板下面是光滑的水平面。由于金属球和木板之间有摩擦（已知摩擦因素为μ），所以要将木板从球下面向右抽出时，至少需要大小为F的水平拉力。试问：现要将木板继续向左插进一些，至少需要多大的水平推力？
解说：这是一个典型的力矩平衡的例题。
以球和杆为对象，研究其对转轴O的转动平衡，设木板拉出时给球体的摩擦力为f ，支持力为N ，重力为G ，力矩平衡方程为：
f R + N（R + L）= G（R + L） ①
球和板已相对滑动，故：f = μN ②
解①②可得：f = 
再看木板的平衡，F = f 。
同理，木板插进去时，球体和木板之间的摩擦f′= 
= F′。
答案：
。
第四讲 摩擦角及其它
一、摩擦角
1、全反力：接触面给物体的摩擦力与支持力的合力称全反力，一般用R表示，亦称接触反力。
2、摩擦角：全反力与支持力的最大夹角称摩擦角，一般用φm表示。
此时，要么物体已经滑动，必有：φm = arctgμ（μ为动摩擦因素），称动摩擦力角；要么物体达到最大运动趋势，必有：φms = arctgμs（μs为静摩擦因素），称静摩擦角。通常处理为φm = φms 。
3、引入全反力和摩擦角的意义：使分析处理物体受力时更方便、更简捷。
二、隔离法与整体法
1、隔离法：当物体对象有两个或两个以上时，有必要各个击破，逐个讲每个个体隔离开来分析处理，称隔离法。
在处理各隔离方程之间的联系时，应注意相互作用力的大小和方向关系。
2、整体法：当各个体均处于平衡状态时，我们可以不顾个体的差异而讲多个对象看成一个整体进行分析处理，称整体法。
应用整体法时应注意“系统”、“内力”和“外力”的涵义。
三、应用
1、物体放在水平面上，用与水平方向成30°的力拉物体时，物体匀速前进。若此力大小不变，改为沿水平方向拉物体，物体仍能匀速前进，求物体与水平面之间的动摩擦因素μ。
解说：这是一个能显示摩擦角解题优越性的题目。可以通过不同解法的比较让学生留下深刻印象。
法一，正交分解。（学生分析受力→列方程→得结果。）
法二，用摩擦角解题。
引进全反力R ，对物体两个平衡状态进行受力分析，再进行矢量平移，得到图18中的左图和中间图（注意：重力G是不变的，而全反力R的方向不变、F的大小不变），φm指摩擦角。
再将两图重叠成图18的右图。由于灰色的三角形是一个顶角为30°的等腰三角形，其顶角的角平分线必垂直底边……故有：φm = 15°。
最后，μ= tgφm 。
答案：0.268 。
（学生活动）思考：如果F的大小是可以选择的，那么能维持物体匀速前进的最小F值是多少？
解：见图18，右图中虚线的长度即Fmin ，所以，Fmin = Gsinφm 。
答：Gsin15°（其中G为物体的重量）。
2、如图19所示，质量m = 5kg的物体置于一粗糙斜面上，并用一平行斜面的、大小F = 30N的推力推物体，使物体能够沿斜面向上匀速运动，而斜面体始终静止。已知斜面的质量M = 10kg ，倾角为30°，重力加速度g = 10m/s2 ，求地面对斜面体的摩擦力大小。
解说：
本题旨在显示整体法的解题的优越性。
法一，隔离法。简要介绍……
法二，整体法。注意，滑块和斜面随有相对运动，但从平衡的角度看，它们是完全等价的，可以看成一个整体。
做整体的受力分析时，内力不加考虑。受力分析比较简单，列水平方向平衡方程很容易解地面摩擦力。
答案：26.0N 。
（学生活动）地面给斜面体的支持力是多少？
解：略。
答：135N 。
应用：如图20所示，一上表面粗糙的斜面体上放在光滑的水平地面上，斜面的倾角为θ。另一质量为m的滑块恰好能沿斜面匀速下滑。若用一推力F作用在滑块上，使之能沿斜面匀速上滑，且要求斜面体静止不动，就必须施加一个大小为P = 4mgsinθcosθ的水平推力作用于斜面体。使满足题意的这个F的大小和方向。
解说：这是一道难度较大的静力学题，可以动用一切可能的工具解题。
法一：隔离法。
由第一个物理情景易得，斜面于滑块的摩擦因素μ= tgθ
对第二个物理情景，分别隔离滑块和斜面体分析受力，并将F沿斜面、垂直斜面分解成Fx和Fy ，滑块与斜面之间的两对相互作用力只用两个字母表示（N表示正压力和弹力，f表示摩擦力），如图21所示。
对滑块，我们可以考查沿斜面方向和垂直斜面方向的平衡——
Fx = f + mgsinθ
Fy + mgcosθ= N
且 f = μN = Ntgθ
综合以上三式得到：
Fx = Fytgθ+ 2mgsinθ ①
对斜面体，只看水平方向平衡就行了——
P = fcosθ+ Nsinθ
即：4mgsinθcosθ=μNcosθ+ Nsinθ
代入μ值，化简得：Fy = mgcosθ ②
②代入①可得：Fx = 3mgsinθ
最后由F =
解F的大小，由tgα= 
解F的方向（设α为F和斜面的夹角）。
答案：大小为F = mg
，方向和斜面夹角α= arctg(
)指向斜面内部。
法二：引入摩擦角和整体法观念。
仍然沿用“法一”中关于F的方向设置（见图21中的α角）。
先看整体的水平方向平衡，有：Fcos(θ- α) = P ⑴
再隔离滑块，分析受力时引进全反力R和摩擦角φ，由于简化后只有三个力（R、mg和F），可以将矢量平移后构成一个三角形，如图22所示。
在图22右边的矢量三角形中，有：
= 
= 
⑵
注意：φ= arctgμ= arctg(tgθ) = θ ⑶
解⑴⑵⑶式可得F和α的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
