
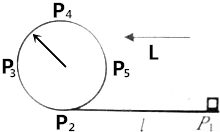
 ��ͼ��ʾΪijͬѧ��Ƶġ��˶��糡��ģ��������ɽ����ʵ���ʾ��ͼ��ֱ���ε���P1P2��뾶ΪR��Բ���ε���ƽ��������P2������װ��ˮƽ̨���ϣ�������̨����̶�����������Ϊm��С��������磬�����ʼ�ձ���Ϊq����ˮƽ̨�����Գ��ٶ�v0��P1λ�ó������ص����˶���������Բ���˶���С������P1P2̨��Ķ�Ħ������Ϊ�̣����ಿ�ֵ�Ħ�����ƣ��������ٶ�Ϊg����ǿ�糡ˮƽ����ǿΪE����Eq�ݦ�mg��P1P2=l������С����ij��ٶȴ�С����������
��ͼ��ʾΪijͬѧ��Ƶġ��˶��糡��ģ��������ɽ����ʵ���ʾ��ͼ��ֱ���ε���P1P2��뾶ΪR��Բ���ε���ƽ��������P2������װ��ˮƽ̨���ϣ�������̨����̶�����������Ϊm��С��������磬�����ʼ�ձ���Ϊq����ˮƽ̨�����Գ��ٶ�v0��P1λ�ó������ص����˶���������Բ���˶���С������P1P2̨��Ķ�Ħ������Ϊ�̣����ಿ�ֵ�Ħ�����ƣ��������ٶ�Ϊg����ǿ�糡ˮƽ����ǿΪE����Eq�ݦ�mg��P1P2=l������С����ij��ٶȴ�С���������� ���� ҪʹС������Բ���˶����������������һ�������С�����������ܵ���ͼ��G�㣮�ڶ��������С����ͨ����Ч��ߵ㣬��������Բ���˶������ݶ��ܶ�����⣮
��� �⣺��������糡���ĺ���ΪF������������F�ļн�Ϊ�ȣ��� tan��=$\frac{qE}{mg}$
�����ڵ糡�����������ȼ���ֱ���˶���P2�㣬�ɶ��ܶ����ã�
qEl-��mgl=$\frac{1}{2}m{v}_{1}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
��һ�������ΪʹС������Բ�����С�����ǡ�õ���G�㣬��P2��G�㣬�ɶ��ܶ����ã�
-mg��R+Rsin�ȣ�+qERcos��=0-$\frac{1}{2}m{v}_{1}^{2}$
������ qEl-��mgl-mg��R+Rsin�ȣ�+qERcos��=-$\frac{1}{2}m{v}_{0}^{2}$��
���� v0=$\sqrt{\frac{2[��mgl+mgR��1+sin�ȣ�-qE��l+Rcos�ȣ�]}{m}}$������ tan��=$\frac{qE}{mg}$��
�ڶ��������F��Ϊ��С���ͬʱ���������͵糡�����µĵ�Ч������������ȷ������С����P1��ʼ���٣�F��Ϊ��Ч��͵㣬��E��Ϊ��Ч��ߵ㣬ΪʹС�������Բ���˶�������ٶ���С��Ҫ��֤С���ǡ��ͨ����Ч��ߵ㣬��E�㣬��
$\sqrt{��qE��^{2}+��mg��^{2}}$=m$\frac{{v}_{2}^{2}}{R}$
��P2��G�㣬�ɶ��ܶ����ã�
-mg��R+Rsin�ȣ�-qERcos��=$\frac{1}{2}m{v}_{2}^{2}$-$\frac{1}{2}m{v}_{1}^{2}$
������ qEl-��mgl-mg��R+Rsin�ȣ�-qERcos��=$\frac{1}{2}$R$\sqrt{��qE��^{2}+��mg��^{2}}$-$\frac{1}{2}m{v}_{0}^{2}$
��� v0=$\sqrt{\frac{R\sqrt{��qE��^{2}+��mg��^{2}}+2[��mgl+mgR��1+sin�ȣ�]-2qE��l-Rcos�ȣ�}{m}}$
���� tan��=$\frac{qE}{mg}$��
��С����ij��ٶȴ�С����������v0��$\sqrt{\frac{2[��mgl+mgR��1+sin�ȣ�-qE��l+Rcos�ȣ�]}{m}}$���� v0��$\sqrt{\frac{R\sqrt{��qE��^{2}+��mg��^{2}}+2[��mgl+mgR��1+sin�ȣ�]-2qE��l-Rcos�ȣ�}{m}}$������ tan��=$\frac{qE}{mg}$��
��С����ij��ٶȴ�С����������v0��$\sqrt{\frac{2[��mgl+mgR��1+sin�ȣ�-qE��l+Rcos�ȣ�]}{m}}$���� v0��$\sqrt{\frac{R\sqrt{��qE��^{2}+��mg��^{2}}+2[��mgl+mgR��1+sin�ȣ�]-2qE��l-Rcos�ȣ�}{m}}$������ tan��=$\frac{qE}{mg}$��
���� ����Ĺؼ�Ҫ�ҳ��ٽ�㣬��ȷ��鲻����Բ�����������������õ�Ч�ķ���������Ч��ߵ���ٽ��������糡���������ĺ����䵱�����������ö��ܶ����о���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
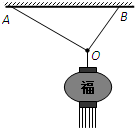 �ҹ����ٵط��ڽ����ڼ��йҺ������ϰ�ף���ͼ������Ϊm�ĵ������������ȳ�������OA��OB������ˮƽ�컨���ϣ�OA��OB����OΪ��㣮�������ٶȴ�СΪg����OA��OB��O��������ֱ�ΪFA��FB�������ܹ������㹻���������������
�ҹ����ٵط��ڽ����ڼ��йҺ������ϰ�ף���ͼ������Ϊm�ĵ������������ȳ�������OA��OB������ˮƽ�컨���ϣ�OA��OB����OΪ��㣮�������ٶȴ�СΪg����OA��OB��O��������ֱ�ΪFA��FB�������ܹ������㹻���������������| A�� | FA����FB | |
| B�� | FA��FB�������mg | |
| C�� | ����������ĵ�����FB����������FA���������� | |
| D�� | ������ε�������A��λ�ã�FA��FB�������ܴ���mg |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
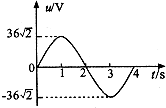 �����߿�����ǿ�ų�������ת�������У��߿�����Ľ�����ѹ��ʱ��仯��ͼ����ͼ��ʾ������˵������ȷ���ǣ�������
�����߿�����ǿ�ų�������ת�������У��߿�����Ľ�����ѹ��ʱ��仯��ͼ����ͼ��ʾ������˵������ȷ���ǣ�������| A�� | ������ѹ����ЧֵΪ36$\sqrt{2}$V | |
| B�� | ������ѹ�����ֵΪ36$\sqrt{2}$V��Ƶ��Ϊ50Hz | |
| C�� | 2sĩ�߿�ƽ�洹ֱ�ڴų���ͨ���߿�Ĵ�ͨ����� | |
| D�� | 1sĩ�߿�ƽ�洹ֱ�ڴų���ͨ���߿�Ĵ�ͨ���仯��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���ڴ�������ʱ���˶Եص��ٶȴ��ڴ��Եص��ٶ� | |
| B�� | ���ڴ�������ʱ���˶Եص��ٶ�С�ڴ��Եص��ٶ� | |
| C�� | ����ֹͣʱ���Ĺ��Դ����Դ�Ҫ�������� | |
| D�� | �˺ʹ���ɵ�ϵͳ�����غ㣬���ܶ��������㣬������ֹͣ��Ҳֹͣ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ������Ϊh�����Ϊd�Ļ���Ԫ������������ֱ�ĴŸ�Ӧǿ�ȴ�СΪB=B0sin��t����ǿ�ų��У����㶨������ͨ������Ԫ��ʱ��������ǰ����������֮�����������磬������ʵ���˽�ֱ������ת��Ϊ���������Ϊ�������Ľ�����ѹ���ɲ�ȡ�Ĵ�ʩ�ǣ�������
��ͼ��ʾ������Ϊh�����Ϊd�Ļ���Ԫ������������ֱ�ĴŸ�Ӧǿ�ȴ�СΪB=B0sin��t����ǿ�ų��У����㶨������ͨ������Ԫ��ʱ��������ǰ����������֮�����������磬������ʵ���˽�ֱ������ת��Ϊ���������Ϊ�������Ľ�����ѹ���ɲ�ȡ�Ĵ�ʩ�ǣ�������| A�� | ����d | B�� | ��Сd | C�� | ����h | D�� | ��Сh |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��X��δ֪����Դ��M�ǵ糡��L�DZ���Ƭ��D�Ǽ��������ֽ�ǿ�糡M�ƿ�������������¼�ļ����ʱ��̲��䣬����ٽ�����ƬL�ƿ�����������ʴ������������XΪ��������
��ͼ��ʾ��X��δ֪����Դ��M�ǵ糡��L�DZ���Ƭ��D�Ǽ��������ֽ�ǿ�糡M�ƿ�������������¼�ļ����ʱ��̲��䣬����ٽ�����ƬL�ƿ�����������ʴ������������XΪ��������| A�� | ���·���Դ | B�� | ���÷���Դ | ||
| C�� | �����µĻ�Ϸ���Դ | D�� | �����õĻ�Ϸ���Դ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �˶�����ڴų���һ�����ܵ����ش��������� | |
| B�� | ���ش����ķ�������������¿������ɵ��˶�����ֱ | |
| C�� | ������˶��ķ������仯ʱ�����ش����ķ���Ҳ��֮�仯 | |
| D�� | ���ش����Ĵ�С���ɵ��˶�����ʹ�������ļн��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �������� | B�� | С������ | C�� | �������� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com