
![]()
图5-17
A.θ B.sinθ C.cosθ D.tanθ
科目:高中物理 来源: 题型:
 (1)一物体静止在水平面上,它的质量是m,与水平面之间的动摩擦因数为μ.用平行于水平面的力F分别拉物体,得到加速度a和拉力F的关系图象如图所示.利用图象可求出这个物体的质量m.
(1)一物体静止在水平面上,它的质量是m,与水平面之间的动摩擦因数为μ.用平行于水平面的力F分别拉物体,得到加速度a和拉力F的关系图象如图所示.利用图象可求出这个物体的质量m.| F |
| a |
| 1 |
| m |
| M1M2 |
| R2 |
| 2π |
| T |
| M1M2 |
| R2 |
| 2π |
| T |
查看答案和解析>>
科目:高中物理 来源: 题型:
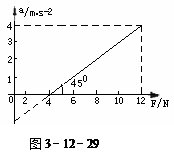 一物体静止在水平面上,它的质量是m,与水平面之间的动摩擦因数为μ.用平行于水平面的力F分别拉物体,得到加速度a和拉力F的关系图象如图3-12-29所示.利用图象可求出这个物体的质量m.
一物体静止在水平面上,它的质量是m,与水平面之间的动摩擦因数为μ.用平行于水平面的力F分别拉物体,得到加速度a和拉力F的关系图象如图3-12-29所示.利用图象可求出这个物体的质量m.
甲同学分析的过程是:从图象中得到F=12N时,物体的加速度a=4m/s2, 根据牛顿定律导出:![]() 得:m=3kg。乙同学的分析过程是:从图象中得出直线的斜率为:k=tan45°=1, 而
得:m=3kg。乙同学的分析过程是:从图象中得出直线的斜率为:k=tan45°=1, 而![]() ,所以m=1kg。请判断甲、乙两个同学结论的对和错,并分析错误的原因。如果两个同学都错,分析各自的错误原因后再计算正确的结果.
,所以m=1kg。请判断甲、乙两个同学结论的对和错,并分析错误的原因。如果两个同学都错,分析各自的错误原因后再计算正确的结果.
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 (1)一物体静止在水平面上,它的质量是m,与水平面之间的动摩擦因数为μ.用平行于水平面的力F分别拉物体,得到加速度a和拉力F的关系图象如图所示.利用图象可求出这个物体的质量m.
(1)一物体静止在水平面上,它的质量是m,与水平面之间的动摩擦因数为μ.用平行于水平面的力F分别拉物体,得到加速度a和拉力F的关系图象如图所示.利用图象可求出这个物体的质量m.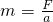 得:m=3kg
得:m=3kg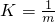 ,所以m=1kg
,所以m=1kg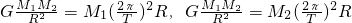 联立解得:M1+M2=…
联立解得:M1+M2=…查看答案和解析>>
科目:高中物理 来源:2006-2007学年广东省四校联考高三(上)期末物理试卷(解析版) 题型:解答题
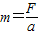 得:m=3kg
得:m=3kg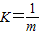 ,所以m=1kg
,所以m=1kg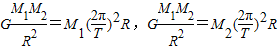 联立解得:M1+M2=…
联立解得:M1+M2=…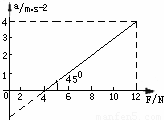
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com