
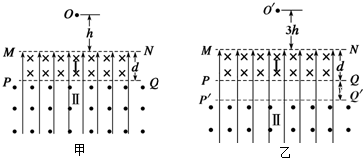
分析 (1)带电小球恰能做匀速圆周运动,则小球所受重力与电场力相等,由此可以求出电场强度.
(2)小求组在混合场中做匀速圆周运动,速率不变,只有小球从进入磁场的位置离开磁场,然后做竖直上抛运动,才有可能回到出发点,由动能定理、牛顿第二定律可以求出释放点的高度.
(3)作出粒子的运动轨迹,作用动能定理、牛顿第二定律、运动学公式,分别求出各阶段的运动时间,然后求出粒子运动的总时间.
解答 解:(1)小球做匀速圆周运动,则mg=qE,电场强度为:E=$\frac{mg}{q}$;
(2)小球从进入磁场的位置离开磁场,才可能回到出发点,小球运动轨迹如图所示;由几何知识得:轨道半径为:R=$\frac{2\sqrt{3}}{3}$d,
小球下落过程中,由动能定理得:mgh=$\frac{1}{2}$mv2-0,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{R}$,
解得:h=$\frac{2{d}^{2}{q}^{2}{B}^{2}}{3g{m}^{2}}$;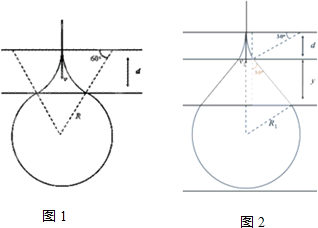 (3)当带电小球从距MN距离为3h处由静止下落时:
(3)当带电小球从距MN距离为3h处由静止下落时:
运动轨迹如图所示,由几何知识可得:R1=2d,
由动能定理得:mg•3h=$\overline{12}$mv12-0,
由牛顿第二定律得:qv1B=m$\frac{{v}_{1}^{2}}{{R}_{1}}$,
粒子在中间运动运动过程中,粒子速度方向与竖直方向成30度角,由几何知识可得:
y=(6-2$\sqrt{3}$)d,
粒子自由落体与竖直上升的总时间为:t1=2$\sqrt{\frac{2×3h}{g}}$=4$\frac{dqB}{mg}$,
粒子做圆周运动的时间为:t2=$\frac{5πm}{3qB}$,
粒子做运动运动的总时间为:t3=2$\frac{2(4\sqrt{3}-4)d}{{v}_{1}}$,
一个来回的总时间为:T=t1+t2+t3=$\frac{4dqB}{mg}$+$\frac{5πm}{3qB}$+$\frac{4(\sqrt{3}-1)m}{qB}$;
答:(1)电场强度为$\frac{mg}{q}$;
(2)小球释放时距MN的高度为$\frac{2{d}^{2}{q}^{2}{B}^{2}}{3g{m}^{2}}$;
(3)磁场Ⅱ向下移动的距离y为:(6-2$\sqrt{3}$)d,带电粒子的运动时间为$\frac{4dqB}{mg}$+$\frac{5πm}{3qB}$+$\frac{4(\sqrt{3}-1)m}{qB}$.
点评 本题是一道难题,分析清楚粒子的运动过程、作出粒子运动轨迹,熟练应用动能定律、牛顿第二定律、数学知识即可正确解题.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
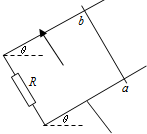 如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1m,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻.匀强磁场方向与导轨平面垂直向上.质量为0.2kg,电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.
如图所示,处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1m,导轨平面与水平面成θ=37°角,下端连接阻值为R的电阻.匀强磁场方向与导轨平面垂直向上.质量为0.2kg,电阻不计的金属棒放在两导轨上,棒与导轨垂直并保持良好接触,它们之间的动摩擦因数为0.25.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
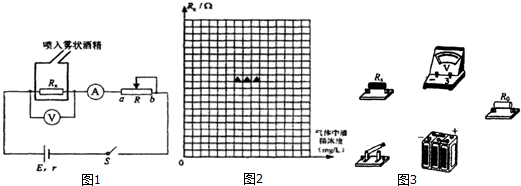
| 实验次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 气体中酒精浓度(mg/L) | 0.0l | 0.02 | 0.04 | 0.06 | 0.07 | 0.09 | 0.12 | 0.15 |
| 电压表示数(V) | 2.00 | 2.40 | 2.20 | 1.60 | 1.40 | 1.20 | 1.00 | 0.86 |
| 电流表示数(A) | 0.10 | 0.15 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 | 0.20 |
| 凡的阻值(Ω) | 20 | 11 | 8 | 7 | 5 | 4.3 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
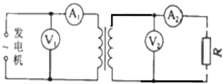 如图所示,理想变压器原线圈匝数n1=3110匝,副线圈匝数n2=311匝,原线圈电压u=311sin100πtV,负载电阻R=44Ω,不计电表对电路的影响,下列说法正确的是( )
如图所示,理想变压器原线圈匝数n1=3110匝,副线圈匝数n2=311匝,原线圈电压u=311sin100πtV,负载电阻R=44Ω,不计电表对电路的影响,下列说法正确的是( )| A. | V2读数为31.1V | |
| B. | A1读数为0.05A | |
| C. | 变压器副线圈两端交变电流的频率为50Hz | |
| D. | 变压器副线圈中磁通量变化率最大值为0.1wb/s |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
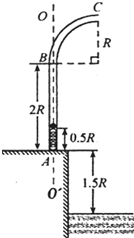 如图为某种鱼饵自动投放器中的投饵管装置示意图,其下半部AB是一长为2R的竖直细管,上半部BC是半径为R的四分之一圆弧弯管,管口沿水平方向,AB管内有一原长为R、下端固定的轻质弹簧.投饵时,每次总将弹簧长度压缩到0.5R后锁定,在弹簧上段放置一粒鱼饵,解除锁定,弹簧可将鱼饵弹射出去.设质量为m的鱼饵到达管口C时,对管壁的作用力恰好为零.不计鱼饵在运动过程中的机械能损失,且锁定和解除锁定时,均不改变弹簧的弹性势能.已知重力加速度为g.求:
如图为某种鱼饵自动投放器中的投饵管装置示意图,其下半部AB是一长为2R的竖直细管,上半部BC是半径为R的四分之一圆弧弯管,管口沿水平方向,AB管内有一原长为R、下端固定的轻质弹簧.投饵时,每次总将弹簧长度压缩到0.5R后锁定,在弹簧上段放置一粒鱼饵,解除锁定,弹簧可将鱼饵弹射出去.设质量为m的鱼饵到达管口C时,对管壁的作用力恰好为零.不计鱼饵在运动过程中的机械能损失,且锁定和解除锁定时,均不改变弹簧的弹性势能.已知重力加速度为g.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
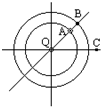 如图所示,在点电荷Q形成的电场中有A、B、C三点,若Q为负电荷,则A点电势最低,将正电荷放在C点时电势能最大,将负电荷放在A点时电势能最大.
如图所示,在点电荷Q形成的电场中有A、B、C三点,若Q为负电荷,则A点电势最低,将正电荷放在C点时电势能最大,将负电荷放在A点时电势能最大.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
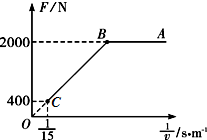 在检测某款电动车性能的某次实验中,质量为8×102㎏的电动车由静止开始沿平直公路行驶,达到的最大速度为15m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象(图中AB、BO均为直线).假设电动车行驶中所受的阻力恒定,求:
在检测某款电动车性能的某次实验中,质量为8×102㎏的电动车由静止开始沿平直公路行驶,达到的最大速度为15m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出F-$\frac{1}{v}$图象(图中AB、BO均为直线).假设电动车行驶中所受的阻力恒定,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com