
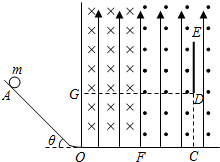
 如图,绝缘轨道的斜面部分倾角为θ=45°,O处由一段小弧平滑连接.点O的右侧空间存在着竖直向上的匀强电场,在OF之间存在垂直纸面向里的匀强电场,在F右侧存在垂直纸面向外的匀强磁场,一质量为m,电荷量为q的绝缘小球从光滑轨道的A点无初速度释放,经过O点后恰好能从G点(GD两点在同一水平线上)射出.已知电场强度E=$\frac{mg}{q}$,左右两侧磁场的磁感强度大小均为B,DE为一处于场中的竖直挡板,OF=FC=CD=DE=L,求:
如图,绝缘轨道的斜面部分倾角为θ=45°,O处由一段小弧平滑连接.点O的右侧空间存在着竖直向上的匀强电场,在OF之间存在垂直纸面向里的匀强电场,在F右侧存在垂直纸面向外的匀强磁场,一质量为m,电荷量为q的绝缘小球从光滑轨道的A点无初速度释放,经过O点后恰好能从G点(GD两点在同一水平线上)射出.已知电场强度E=$\frac{mg}{q}$,左右两侧磁场的磁感强度大小均为B,DE为一处于场中的竖直挡板,OF=FC=CD=DE=L,求:分析 (1)根据题求出小球在磁场中做圆周运动的轨道半径,由牛顿第二定律求出小球做圆周运动的速度,然后由机械能守恒定律求出小球释放点的高度.
(2)应用牛顿第二定律与机械能守恒定律求出小球释放点的两个临界高度,然后求出释放点到O点的临界距离,然后确定距离范围.
解答 解:(1)小球在电磁场中受到竖直向下的重力mg,竖直向上的电场力:qE=mg,
重力与电场力合力为零,则小球在洛伦兹力作用下做匀速圆周运动,
小球恰好能从G点射出磁场,则小球做圆周运动的轨道半径:r1=$\frac{L}{2}$,
由牛顿第二定律得:qv1B=m$\frac{{v}_{1}^{2}}{{r}_{1}}$,
小球从A到O过程,由机械能守恒定律得:mgh1=$\frac{1}{2}$mv12,
解得:h1=$\frac{{q}^{2}{B}^{2}{L}^{2}}{8{m}^{2}g}$;
(2)①如果小球打在E点,则小球做圆周运动的轨道半径:r=L,
由牛顿第二定律得:qvB=m$\frac{{v}^{2}}{r}$,
小球凑个释放到O点过程,由机械能守恒定律得:mgh=$\frac{1}{2}$mv2,
解得:h=$\frac{{q}^{2}{B}^{2}{L}^{2}}{2{m}^{2}g}$;
②如果小球打在D点,由几何知识得:r′2=L2+(r$′-\frac{L}{2}$)2,
由牛顿第二定律得:qv′B=m$\frac{v{′}^{2}}{r′}$,
小球凑个释放到O点过程,由机械能守恒定律得:mgh′=$\frac{1}{2}$mv′2,
解得:h′=$\frac{25{q}^{2}{B}^{2}{L}^{2}}{32{m}^{2}g}$;
释放点距O点的距离:x=$\frac{h}{sin45°}$=$\sqrt{2}$h,
则释放点到O点的距离:$\frac{\sqrt{2}{q}^{2}{B}^{2}{L}^{2}}{2{m}^{2}g}$≤x≤$\frac{25\sqrt{2}{q}^{2}{B}^{2}{L}^{2}}{32{m}^{2}g}$
答:(1)小球开始释放的高度是:$\frac{{q}^{2}{B}^{2}{L}^{2}}{8{m}^{2}g}$;
(2)要使小球打在DE挡板上,小球m在斜面上离O点的多大范围是:$\frac{\sqrt{2}{q}^{2}{B}^{2}{L}^{2}}{2{m}^{2}g}$≤x≤$\frac{25\sqrt{2}{q}^{2}{B}^{2}{L}^{2}}{32{m}^{2}g}$.
点评 本题考查了带电小球在复合场中的运动,分析清楚小球的运动过程是正确解题的关键,分析清楚小球的受力情况是正确解题的前提,应用牛顿第二定律与机械能守恒定律可以解题,解题时要注意几何知识的应用.


科目:高中物理 来源: 题型:多选题
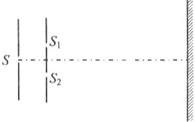
| A. | 如果用白光照射单缝S,将在屏上看到亮暗相间的条纹 | |
| B. | 如果用白光照射单缝S,将在屏上看到彩色条纹 | |
| C. | 如果用普通白炽灯发出的光做实验,撤去单缝S后仍然可以观察到干涉现象 | |
| D. | 如果用激光器发出的单色光做实验,撤去单缝S后仍然可以观察到干涉现象 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
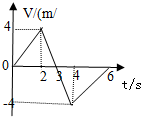
| A. | 0-2秒物体的加速度是1m/s2 | B. | 2-4秒物体做匀减速运动 | ||
| C. | 3-4秒物体做反向匀加速运动 | D. | 4-6秒物体做匀加速运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:填空题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
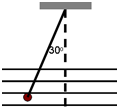 一个质量m=30g,带电荷量为q=-2×10-8C的半径极小的小球,用丝线悬挂在某匀强电场中,电场线水平.当小球静止时,测得悬线与竖直方向成30°夹角,如图所示,求该电场的场强大小,并说明场强方向.
一个质量m=30g,带电荷量为q=-2×10-8C的半径极小的小球,用丝线悬挂在某匀强电场中,电场线水平.当小球静止时,测得悬线与竖直方向成30°夹角,如图所示,求该电场的场强大小,并说明场强方向.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| I/A | 0.12 | 0.20 | 0.31 | 0.32 | 0.50 | 0.57 |
| U/V | 1.37 | 1.32 | 1.24 | 1.18 | 1.10 | 1.05 |
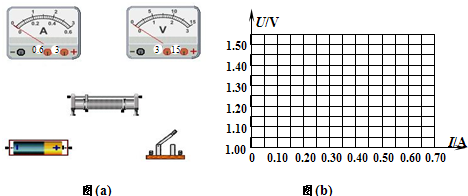
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com