
 如图所示,质量为m的小球置于正方体的质量为M的光滑盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计.
如图所示,质量为m的小球置于正方体的质量为M的光滑盒子中,盒子的边长略大于球的直径.某同学拿着该盒子在竖直平面内做半径为R的匀速圆周运动,已知重力加速度为g,空气阻力不计.分析 (1)在最高点,盒子与小球之间无作用力,知小球靠重力提供向心力,结合牛顿第二定律求出角速度的大小;
(2)分别在最低点和最高点,根据牛顿第二定律列式求解F1和F2,进而求出(F2-F1),从而画出(F2-F1)-ω2图象;
(3)当盒子运动到与圆心等高的位置时,这位同学对盒子作用力的水平分力F′提供向心力,竖直分力F″与重力平衡,据此列式求解.
解答 解:(1)要使在最高点时盒子与小球之间恰好无作用力,由重力提供向心力,则有mg=mRω2
解得:ω=$\sqrt{\frac{g}{R}}$
(2)当ω≤$\sqrt{\frac{g}{R}}$时,
${F}_{2}-mg=m{ω}^{2}R$,
mg-F1=mω2R
解得:F2-F1=2mRω2
当ω>$\sqrt{\frac{g}{R}}$时,${F}_{2}-mg=m{ω}^{2}R$,
${F}_{1}+mg=m{ω}^{2}R$
解得F2-F1=2mg
则(F2-F1)-ω2图象如图所示: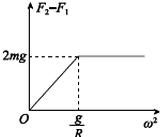
(3)当盒子运动到与圆心等高的位置时,这位同学对盒子作用力的水平分力F′提供向心力,竖直分力F″与重力平衡,即
F′=(M+m)Rω2,F″=(M+m)g
则该同学对盒子的作用力为F=$\sqrt{F{′}^{2}+F{″}^{2}}=(m+M)\sqrt{{R}^{2}{ω}^{4}+{g}^{2}}$
答:(1)要使在最高点时盒子与小球之间恰好无作用力,盒子做圆周运动的角速度为$\sqrt{\frac{g}{R}}$;
(2)(F2-F1)-ω2图象如图所示.
(3)盒子运动到与圆心等高的位置时,这位同学对盒子的作用力为$(m+M)\sqrt{{R}^{2}{ω}^{4}+{g}^{2}}$.
点评 解决本题的关键知道小球在最高点和最低点的向心力来源,结合牛顿第二定律进行求解,难度适中.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:高中物理 来源: 题型:选择题
| A. | 乙质点比甲质点位置变化慢 | |
| B. | 因为2>-4,所以甲质点的速度大于乙质点的速度 | |
| C. | 这里正负号的物理意义是表示运动的方向 | |
| D. | 若甲、乙两质点同时由同一点出发,则10s后甲、乙两质点相距20m |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
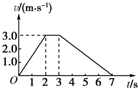
| A. | 物体在加速阶段的加速度大小为1.5 m/s2 | |
| B. | 物体在减速阶段的加速度大小为1 m/s2 | |
| C. | 第3 s内物体的位移为3 m | |
| D. | 物体在加速过程的位移等于减速过程的位移 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 在如图所示的电路中,电源的负极接地,其电动势为E、内阻为r,R1、R2为定值电阻,R3为滑动变阻器,C为电容器,
在如图所示的电路中,电源的负极接地,其电动势为E、内阻为r,R1、R2为定值电阻,R3为滑动变阻器,C为电容器, 、
、 为理想电流表和电压表.在滑动变阻器滑片P自a端向b端滑动的过程中,下列说法中正确的是( )
为理想电流表和电压表.在滑动变阻器滑片P自a端向b端滑动的过程中,下列说法中正确的是( )| A. | 电源的输出功率减小 | B. | 电流表的示数变大 | ||
| C. | a点的电势升高 | D. | 电容器C所带的电荷量增多 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 元电荷就是电子 | B. | 元电荷就是质子 | ||
| C. | 元电荷的值通常取e=1.60×10-19C | D. | 元电荷的值通常取e=1.60×10-23C |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,悬挂的金属圆环C与通电螺线管在同一轴线上,当滑片向左滑动时,圆环C向左还是向右摆动?圆环有扩张趋势还是收缩趋势?若将金属圆环C悬挂在螺线管的中间,如图中虚线所示位置,则又如何?
如图所示,悬挂的金属圆环C与通电螺线管在同一轴线上,当滑片向左滑动时,圆环C向左还是向右摆动?圆环有扩张趋势还是收缩趋势?若将金属圆环C悬挂在螺线管的中间,如图中虚线所示位置,则又如何?查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. | A与B同时由静止出发,朝相反的方向运动 | |
| B. | 在t=4s时A与B相遇 | |
| C. | t=2s时,A与B两质点间距离一定等于2m | |
| D. | 前4s内,B的平均速度为0.75m/s |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com