一名宇航员抵达某星球后,测得:①载人飞船环绕该星球表面n圈所用的时间为t;②摆长为l的单摆在该星球上的周期为T.已知万有引力恒量为G,不计阻力.试根据题中所提供的条件和测量结果,求:
(1)环绕该星球飞行的卫星的最小周期;
(2)该星球的密度;
(3)该星球的第一宇宙速度是多大?
【答案】
分析:(1)根据题意求出载人飞船绕星球表面做圆周运动的周期,该周期是飞船绕星球运动的最小周期;
(2)载人飞船绕星球做圆周运动的向心力由万有引力提供,由牛顿第二定律列方程可以求出星球的质量,然后由密度公式求出星球的密度;
(3)由单摆的周期公式求出星球表面的重力加速度,星球表面的物体受到的重力等于万有引力,
绕星球表面做圆周运动的速度是第一宇宙速度,根据万有引力公式列方程,求出该星球的第一宇宙速度.
解答:解:(1)载人飞船绕星球表面运动时,轨道半径最小,周期最小,
由题意知,环绕该星球飞行的卫星的最小周期T
最小=
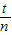
;
(2)设星球的质量为M,半径是R,载人飞船质量是m,载人飞船绕星球表面做圆周运动,
轨道半径等于星球半径,载人飞船绕星球做匀速圆周运动的向心力由万有引力提供,
由牛顿第二定律得:G
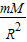
=m
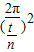
R,
星球质量M=
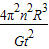
①,
星球的密度ρ=
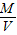
=

=
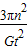
;
(3)单摆的周期T=2π
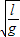
,
则星球表面的重力加速度g=
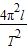
,
位于星球表面的物体m′受到的重力等于万有引力,
即:m′g=G
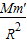
,则GM=gR
2 ②,
由①②得:R=
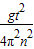
③;
卫星绕星球表面做圆周运动时,即轨道半径等于星球半径时的速度是第一宇宙速度,
万有引力提供向心力,由牛顿第二定律得:
G
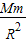
=m

,
v=
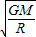
=
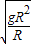
=
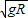
=
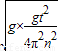
=g
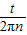
=
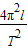
×
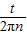
=
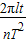
;
答:(1)环绕该星球飞行的卫星的最小周期是
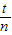
.
(2)该星球的密度是
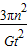
.
(3)该星球的第一宇宙速度是
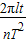
.
点评:卫星绕行星表面做圆周运动的速度是第一宇宙速度,卫星做圆周运动时,万有引力提供向心力,解题时注意单摆周期公式的应用,注意黄金代换的应用.

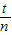 ;
;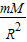 =m
=m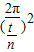 R,
R,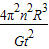 ①,
①,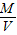 =
= =
=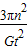 ;
;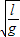 ,
,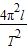 ,
,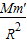 ,则GM=gR2 ②,
,则GM=gR2 ②,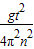 ③;
③;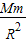 =m
=m ,
,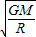 =
=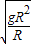 =
=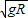 =
=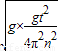 =g
=g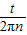 =
=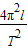 ×
×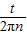 =
=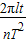 ;
;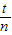 .
.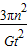 .
.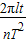 .
.
