
 ��ͼ��ʾ�����Ϊ�ȵĹ⻬б��˹̶�һ���Ե���P����С����A��B��б���Ͼ൲��P�ֱ�Ϊl��3l��λ��ͬʱ�ɾ�ֹ�ͷţ�A�뵲����ײ����ԭ���ʷ��أ�A��B����ײʱ�伫������е����ʧ����֪A������Ϊ3m��B������Ϊm���������ٶ�Ϊg��������ײǰ����һ��ֱ�����˶������Կ�����������ײʱ�䣬��������Ϊ�ʵ㣬��
��ͼ��ʾ�����Ϊ�ȵĹ⻬б��˹̶�һ���Ե���P����С����A��B��б���Ͼ൲��P�ֱ�Ϊl��3l��λ��ͬʱ�ɾ�ֹ�ͷţ�A�뵲����ײ����ԭ���ʷ��أ�A��B����ײʱ�伫������е����ʧ����֪A������Ϊ3m��B������Ϊm���������ٶ�Ϊg��������ײǰ����һ��ֱ�����˶������Կ�����������ײʱ�䣬��������Ϊ�ʵ㣬������ ��1������ţ�ٵڶ������������������б�����˶�ʱ�ļ��ٶȣ���λ�ƹ�ʽ���A�˶���P��ʱ�䣬���ٶȹ�ʽ���A�˶���P���ٶȣ��ٸ�������ʱλ�ƹ�ϵ��ʽ�����˶�ʱ�䣬����λ�ƹ�ʽ����������һ��������λ�õ�P�ľ��룮
��2���Ƚ������Ľ�������ٶȹ�ʽ�����������ײǰ˲����ٶȣ��ٸ��ݵ�����ײ�Ĺ��ɣ������غ�Ͷ����غ���ʽ���������˲�����ߵ��ٶȣ������˶�ѧ��ʽ��B�뵲�����Զ���룮
��� �⣺��1����������б�����˶�ʱ�����ٶ���ͬ����Ϊa����ţ�ٵڶ������У�
mgsin��=ma
�ã�a=gsin��
��A�˶���P��ʱ��Ϊt1���ٶ�Ϊv1�����У�
l=$\frac{1}{2}a{t}_{1}^{2}$��v1=at1��
��ã�t1=$\sqrt{\frac{2l}{a}}$��v1=$\sqrt{2al}$
A�뵲����ײ��������v1��б�����ϻ�������A���پ���ʱ��t2��B�����������㵽P�ľ���Ϊx�����˶�ѧ���ɵã�
x=v1t2-$\frac{1}{2}a{t}_{2}^{2}$
B��б�������ȼ����˶������˶�ѧ�����У�
3l-x=$\frac{1}{2}a��{t}_{1}+{t}_{2}��^{2}$
��ã�t2=$\sqrt{\frac{l}{2a}}$��x=$\frac{3}{4}$l
��2����A��B��ײǰ���ٶȴ�С�ֱ�ΪvA��vB�����У�
vA=v1-at2��
vB=a��t1+t2��
��ã�vA=$\sqrt{\frac{al}{2}}$��������б�����ϣ�vB=3$\sqrt{\frac{al}{2}}$��������б�����£�
��A��B��ײ����ٶȷֱ�ΪvA���vB�䣬�涨��б������Ϊ�������ɶ����غ㶨�ɺͻ�е���غ㶨���У�
3mvA-mvB=3mvA��+mvB��
$\frac{1}{2}•$3mvA2+$\frac{1}{2}$mvB2=$\frac{1}{2}•$3mvA��2+$\frac{1}{2}$mvB��2
��ã�vA��=-$\sqrt{\frac{al}{2}}$��vB��=3$\sqrt{\frac{al}{2}}$
��һ��������B�ϻ��ľ���ΪxB�����У�
0-vB��2=-2axB��
B�뵲�����Զ����Ϊ��
xm=x+xB
��ã�xm=3l
�𣺣�1���������һ��������λ�õ�P�ľ���Ϊ$\frac{3}{4}$l��
��2���������һ��������B�뵲�����Զ������3l��
���� �������Ĺؼ�����������������˶����̣�����ţ�ٵڶ����ɺ��˶�ѧ��ʽ����߷�����Ҫ��������ʱ���ߵ�λ�ƹ�ϵ�����ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
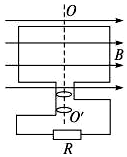 ��ͼ��ʾ����һ������Ȧ���ΪS������ΪN������Ϊr����OO�����Խ��ٶȦ�������ת������������ͼ��ʾλ��ת��90��Ĺ����У�����˵������ȷ���ǣ�������
��ͼ��ʾ����һ������Ȧ���ΪS������ΪN������Ϊr����OO�����Խ��ٶȦ�������ת������������ͼ��ʾλ��ת��90��Ĺ����У�����˵������ȷ���ǣ�������| A�� | ��ͼʾλ�ÿ�ʼ��ʱ����Ӧ�綯����ʱ��仯�Ĺ���Ϊe=NBS��sin��t | |
| B�� | ��Ȧ�е�������ЧֵΪI=$\frac{NBS��}{��R+r��}$ | |
| C�� | ͨ������ĵ����ΪQ=$\frac{NBS}{��R+r��}$ | |
| D�� | �ڵ���R�ϲ������ȹ���Ϊp=$\frac{{N}^{2}{B}^{2}{S}^{2}��}{2��R+r��}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
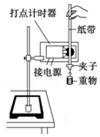 ��ͼ��ʾ�����ش������������˶�������֤��е���غ㶨�ɡ���ʵ��װ�ã�
��ͼ��ʾ�����ش������������˶�������֤��е���غ㶨�ɡ���ʵ��װ�ã��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��������г�˶��Ļظ������������������ĺ����ṩ | |
| B�� | ��������г�˶�������������Ͱڳ��й� | |
| C�� | ���������˶������Ƶ�ʵ��������Ĺ���Ƶ��ʱ���������� | |
| D�� | ��е���������ٶȵ��ڲ����ʵ����ٶ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
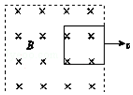 ��ͼ��ʾ���Ⱥ����ٶ�v1��v2���ٰ�һ������Ȧˮƽ�����н���ǿ�ų�������v1=2v2�������Ⱥ���������£�������
��ͼ��ʾ���Ⱥ����ٶ�v1��v2���ٰ�һ������Ȧˮƽ�����н���ǿ�ų�������v1=2v2�������Ⱥ���������£�������| A�� | ��Ȧ�еĸ�Ӧ�綯��֮��ΪE1��E2=1��2 | |
| B�� | ��Ȧ�еĸ�Ӧ����֮��ΪI1��I2=1��2 | |
| C�� | ��Ȧ�в����Ľ�����֮��Q1��Q2=1��4 | |
| D�� | ͨ����Ȧij����ĵ����֮��q1��q2=1��1 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
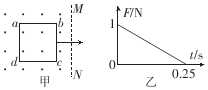 ��ͼ����ʾ���ڴŸ�Ӧǿ��B=lT���н���ǿ�ų��У����������߳�1=0.5m�������ν����߿�������ȫ��ͬ���������������ų�����bc�߸��뿪�ų���ʱ��Ϊ��ʱ��㣬���߿���ئ�ų��Ĺ����У�ab���ܵ��İ�������СF��ʱ��t�仯�Ĺ�ϵ��ͼ����ʾ��������˵����ȷ���ǣ�������
��ͼ����ʾ���ڴŸ�Ӧǿ��B=lT���н���ǿ�ų��У����������߳�1=0.5m�������ν����߿�������ȫ��ͬ���������������ų�����bc�߸��뿪�ų���ʱ��Ϊ��ʱ��㣬���߿���ئ�ų��Ĺ����У�ab���ܵ��İ�������СF��ʱ��t�仯�Ĺ�ϵ��ͼ����ʾ��������˵����ȷ���ǣ�������| A�� | �߿��������˶����ٶȴ�СΪ2m/s | |
| B�� | �߿�����ĸ�Ӧ����Ϊ��ʱ�뷽��СΪ0.5 A | |
| C�� | �����߿���ܵ���Ϊ0.5�� | |
| D�� | �߿��ų������в����Ľ�����Ϊ0.5 J |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
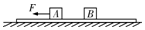 һ�����ʱ�ӲֽƬ���ڹ⻬ˮƽ�����ϣ�ֽƬ�Ϸ���������Ϊ 1kg ��A��B����飬A��B�뱡ӲֽƬ֮��Ķ�Ħ�������ֱ�Ϊ��1=0.2����2=0.3��ˮƽ����F������A����ϣ���ͼ��ʾ����֪���Ħ�������ڻ���Ħ������g=10m/s2��������
һ�����ʱ�ӲֽƬ���ڹ⻬ˮƽ�����ϣ�ֽƬ�Ϸ���������Ϊ 1kg ��A��B����飬A��B�뱡ӲֽƬ֮��Ķ�Ħ�������ֱ�Ϊ��1=0.2����2=0.3��ˮƽ����F������A����ϣ���ͼ��ʾ����֪���Ħ�������ڻ���Ħ������g=10m/s2��������| A�� | ��F=1 N������顢��ӲֽƬ����ֹ���� | |
| B�� | ��F=1.5 N����A�������Ħ������СΪ1.5 N | |
| C�� | ��F=8 N����B���ļ��ٶ�Ϊ4.0 m/s2 | |
| D�� | ������F���B�뱡ӲֽƬ֮�䶼���ᷢ����Ի��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
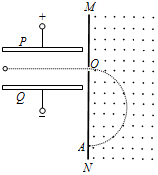 ��ͼ��ʾ����ƽ�н�����P��Qˮƽ���ã��ϼ�������磬�¼�������磻��������ǿ�糡����ǿ�ų���ͼ��δ��������һ�������������������������ʾ·��������ֱ���˶�������ͨ����ƽ�а���O�㴹ֱ������һ����ֱֽ���������ǿ�ų��У�����������Բ���˶�������������ں���ڵ���MN�ϵ�A�㣮��������������������˵������ȷ���ǣ�������
��ͼ��ʾ����ƽ�н�����P��Qˮƽ���ã��ϼ�������磬�¼�������磻��������ǿ�糡����ǿ�ų���ͼ��δ��������һ�������������������������ʾ·��������ֱ���˶�������ͨ����ƽ�а���O�㴹ֱ������һ����ֱֽ���������ǿ�ų��У�����������Բ���˶�������������ں���ڵ���MN�ϵ�A�㣮��������������������˵������ȷ���ǣ�������| A�� | ������һ�������� | |
| B�� | P��Q��Ĵų�һ����ֱֽ������ | |
| C�� | ����һ����������Ҳ��������ֱ���˶�������һ��������Ӿ�����ͬ�ĺ��ʱ� | |
| D�� | ����һ����������Ҳ������ͬ�Ĺ켣�˶�������һ��������Ӿ�����ͬ�ĺ��ʱ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com