
 如图所示,竖直放置的半圆形轨道与水平轨道平滑连接,不计一切摩擦.圆心O点正下方放置为2m的小球A,质量为m的小球B以初速度v0向左运动,与小球A发生弹性碰撞.碰后小球A在半圆形轨道运动时不脱离轨道,则小球B的初速度v0可能为( )
如图所示,竖直放置的半圆形轨道与水平轨道平滑连接,不计一切摩擦.圆心O点正下方放置为2m的小球A,质量为m的小球B以初速度v0向左运动,与小球A发生弹性碰撞.碰后小球A在半圆形轨道运动时不脱离轨道,则小球B的初速度v0可能为( )| A. | 2$\sqrt{2gR}$ | B. | $\sqrt{2gR}$ | C. | 2$\sqrt{5gR}$ | D. | $\sqrt{5gR}$ |
分析 小球A的运动可能有两种情况:1.恰好能通过最高点,说明小球到达最高点时小球的重力提供向心力,由牛顿第二定律求出小球到达最高点点的速度,由机械能守恒定律可以求出碰撞后小球A的速度.由碰撞过程中动量守恒及能量守恒定律可以求出小球B的初速度;
2.小球不能到达最高点,则小球不脱离轨道时,恰好到达与O等高处,由机械能守恒定律可以求出碰撞后小球A的速度.由碰撞过程中动量守恒及能量守恒定律可以求出小球B的初速度.
解答 解:A与B碰撞的过程为弹性碰撞,则碰撞的过程中动量守恒,设B的初速度方向为正方向,设碰撞后B与A的速度分别为v1和v2,则:
mv0=mv1+2mv2
由动能守恒得:
$\frac{1}{2}m{v}_{0}^{2}=\frac{1}{2}m{v}_{1}^{2}+\frac{1}{2}•2m{v}_{2}^{2}$
联立得:${v}_{2}=\frac{2}{3}{v}_{0}$ ①
1.恰好能通过最高点,说明小球到达最高点时小球的重力提供向心力,是在最高点的速度为vmin,由牛顿第二定律得:
$2mg=\frac{2m{v}_{min}^{2}}{R}$ ②
A在碰撞后到达最高点的过程中机械能守恒,得:
$\frac{1}{2}•2m{v}_{2}^{2}=\frac{1}{2}•2m{v}_{min}^{2}+2mg•2R$ ③
联立①②③得:${v}_{0}=1.5\sqrt{5gR}$,可知若小球B经过最高点,则需要:${v}_{0}≥1.5\sqrt{5gR}$
2.小球不能到达最高点,则小球不脱离轨道时,恰好到达与O等高处,由机械能守恒定律得:
$\frac{1}{2}•2m{v}_{2}^{2}=2mgR$④
联立①④得:${v}_{0}=1.5\sqrt{2gR}$
可知若小球不脱离轨道时,需满足:${v}_{0}≤1.5\sqrt{2gR}$
由以上的分析可知,若小球不脱离轨道时,需满足:${v}_{0}≤1.5\sqrt{2gR}$或${v}_{0}≥1.5\sqrt{5gR}$,故AD错误,BC正确.
故选:BC
点评 熟练应用牛顿第二定律、机械能守恒定律、动量守恒定律即可正确解题,注意小球A的运动过程中不脱离轨道可能有两种情况,难度适中.


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:多选题
 小球A和B用细线连接,可以在光滑的水平杆上无摩擦地滑动,已知它们的质量之比m1:m2=3:1,当这一装置绕着竖直轴做匀速转动且A、B两球与水平杆子达到相对静止时(如图),A、B两球做匀速圆周运动的( )
小球A和B用细线连接,可以在光滑的水平杆上无摩擦地滑动,已知它们的质量之比m1:m2=3:1,当这一装置绕着竖直轴做匀速转动且A、B两球与水平杆子达到相对静止时(如图),A、B两球做匀速圆周运动的( )| A. | 线速度大小相等 | B. | 半径之比为r1:r2=1:3 | ||
| C. | 角速度相等 | D. | 向心力的大小之比为F1:F2=3:1 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图1所示水平放置的气缸内被活塞封闭一定质量的理想气体,气体的温度为17℃,活塞与气缸底的距离L1=12cm,离气缸口的距离L2=3cm,将气缸缓慢地转到开口向上的竖直位置,待稳定后对缸内气体逐渐加热,使活塞上表面刚好与气缸口相平为止如图2所示.已知g=10m/s2,大气压强为1.0×105 Pa,活塞的横截面积S=100cm2,质量m=20kg,活塞可沿气缸壁无摩擦滑动但不漏气,求:
如图1所示水平放置的气缸内被活塞封闭一定质量的理想气体,气体的温度为17℃,活塞与气缸底的距离L1=12cm,离气缸口的距离L2=3cm,将气缸缓慢地转到开口向上的竖直位置,待稳定后对缸内气体逐渐加热,使活塞上表面刚好与气缸口相平为止如图2所示.已知g=10m/s2,大气压强为1.0×105 Pa,活塞的横截面积S=100cm2,质量m=20kg,活塞可沿气缸壁无摩擦滑动但不漏气,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 冲击摆是用来测量子弹速度的一种简单装置.如图所示,将一个质量很大的砂箱用轻绳悬挂起来,一颗子弹水平射入砂箱,砂箱发生摆动.若子弹射击砂箱时的速度为v,测得冲击摆的最大摆角为θ,砂箱上升的最大高度为h,则当子弹射击砂箱时的速度变为2v时,下列说法正确的是( )
冲击摆是用来测量子弹速度的一种简单装置.如图所示,将一个质量很大的砂箱用轻绳悬挂起来,一颗子弹水平射入砂箱,砂箱发生摆动.若子弹射击砂箱时的速度为v,测得冲击摆的最大摆角为θ,砂箱上升的最大高度为h,则当子弹射击砂箱时的速度变为2v时,下列说法正确的是( )| A. | 冲击摆的最大摆角将变为2θ | |
| B. | 冲击摆的最大摆角的正切值将变为2tanθ | |
| C. | 砂箱上升的最大高度将变为2h | |
| D. | 砂箱上升的最大高度将变为4h |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
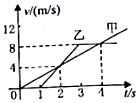
| A. | 甲乙两车同时从静止开始出发 | B. | 在t=2s时乙车追上甲车 | ||
| C. | 在t=4s时乙车追上甲车 | D. | 甲乙两车在公路上可能相遇两次 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图,两条水平虚线之间有垂直于纸面向里、宽度为d、磁感应强度为B的匀强磁场.质量为m、电阻为R的正方形线圈边长为L(L<d),线圈下边缘到磁场上边界的距离为h.将线圈由静止释放,其下边缘刚进入磁场和刚穿出磁场时刻的速度都是v0在整个线圈穿过磁场的全过程中(从下边缘进入磁场到上边缘穿出磁场),下列说法中正确的是( )
如图,两条水平虚线之间有垂直于纸面向里、宽度为d、磁感应强度为B的匀强磁场.质量为m、电阻为R的正方形线圈边长为L(L<d),线圈下边缘到磁场上边界的距离为h.将线圈由静止释放,其下边缘刚进入磁场和刚穿出磁场时刻的速度都是v0在整个线圈穿过磁场的全过程中(从下边缘进入磁场到上边缘穿出磁场),下列说法中正确的是( )| A. | 线圈可能先加速后减速 | B. | 线圈的最小速度可能是$\frac{mgR}{{B}^{2}{L}^{2}}$ | ||
| C. | 线圈的最小速度一定是$\sqrt{2g(h-d+L)}$ | D. | 线圈产生的焦耳热为2mgd |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. |  | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com