
���� �����ȱ���ֱ���˶����ٶ�λ�ƹ�ʽ�ֱ��������4mʱ��������10mʱ���ٶȣ�������ι����е�ʱ�䣬����λ��ʱ�乫ʽ����ָ��������ʱ���ڵ�λ�ƣ��Ӷ��ó����һ�ι����е�λ�ƣ����λ��ʱ�乫ʽ������һ�ι����е�ʱ�䣬�Ӷ��ó���ʱ�䣮
��� �⣺���ɻ�������L1=4mʱ���ٶ�Ϊ��${v}_{1}=\sqrt{2{a}_{1}{L}_{1}}$=$\sqrt{2��2��4}$m/s=4m/s��
������ʱ��Ϊ��${t}_{1}=\frac{{v}_{1}}{{a}_{1}}=\frac{4}{2}s=2s$��
������L2=10mʱ���ٶ�Ϊ��${v}_{2}=\sqrt{{{v}_{1}}^{2}+2{a}_{2}{L}_{2}}$=$\sqrt{16+2��1��10}m/s=6m/s$��
������ʱ��Ϊ��${t}_{2}=\frac{{v}_{2}-{v}_{1}}{{a}_{2}}=\frac{6-4}{1}s=2s$��
ʧȥ����������tʱ���ڵ�λ��Ϊ��${L}_{3}={v}_{2}��t-\frac{1}{2}{a}_{3}��{t}^{2}$=$6��1-\frac{1}{2}��8��1m$=2m��
�ٶ�Ϊ��v3=v2-a3��t=6-8��1m/s=-2m/s��
���һ�ε�λ��Ϊ��L4=L-L1-L2-L3=46-4-10-2m=30m��
����${L}_{4}={v}_{3}{t}_{4}+\frac{1}{2}{a}_{2}{{t}_{4}}^{2}$
�ã�$30=-2{t}_{4}+\frac{1}{2}��1��{{t}_{4}}^{2}$��
���t4=10s��
��t=t1+t2+��t+t4s=2+2+1+10s=15s��
�𣺷ɻ���Ҫ15sʱ��ſ��Է���ƽ̨���ڵ�λ�ã�
���� �������Ĺؼ�����ɻ������������е��˶����ɣ�����˶�ѧ���ٶ�ʱ�乫ʽ��λ��ʱ�乫ʽ���ٶ�λ�ƹ�ʽ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
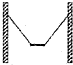 ��ͼ������������Ϊ2d����������Ϊd������Ϊm�ľ���ľ�������ڼ��Ϊ3d��ֱľ�ϵȸߵ����㣬�Ƴ�һ������ǧ��ij��ά��ʱ����һ�鳤Ϊ2d������Ϊ$\sqrt{\frac{6}{5}}m$ľ�彫ԭľ�廻�������ӵ����ҵ㻹��ľ������˵㣬ľ�徲ֹʱ��F1��ʾľ�����ܺ�����С��F2��ʾ����������δ�������Ĵ�С����ά������
��ͼ������������Ϊ2d����������Ϊd������Ϊm�ľ���ľ�������ڼ��Ϊ3d��ֱľ�ϵȸߵ����㣬�Ƴ�һ������ǧ��ij��ά��ʱ����һ�鳤Ϊ2d������Ϊ$\sqrt{\frac{6}{5}}m$ľ�彫ԭľ�廻�������ӵ����ҵ㻹��ľ������˵㣬ľ�徲ֹʱ��F1��ʾľ�����ܺ�����С��F2��ʾ����������δ�������Ĵ�С����ά������| A�� | F1����F2���� | B�� | F1���䣬F2���� | C�� | F1���䣬F2��С | D�� | F1���䣬F2���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���о�������ͧ�����й켣ʱ�����ܽ��俴���ʵ� | |
| B�� | ��5ǧ�ຣ�ָ���ǻ�����ͧ�ĺ���λ�� | |
| C�� | ��5ǧ�ຣ�ָ���ǻ�����ͧ�ĺ���·�� | |
| D�� | ���������������ǿ�����ô˴κ��е�ƽ���ٶ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ����Դ�綯��ΪE������Ϊr�����·�ܵ���ΪR����S�պϺ�Դ�ܹ���Ϊ$\frac{{E}^{2}}{R+r}$����Դ���������Ϊ$\frac{{E}^{2}R}{��R+r��^{2}}$�����·���ĵĹ���Ϊ$\frac{{E}^{2}R}{��R+r��^{2}}$���ڲ����ĵĹ���Ϊ$\frac{{E}^{2}r}{��R+r��^{2}}$����Դ�Ĺ���Ч��Ϊ$\frac{R}{R+r}$��100%��
��ͼ��ʾ����Դ�綯��ΪE������Ϊr�����·�ܵ���ΪR����S�պϺ�Դ�ܹ���Ϊ$\frac{{E}^{2}}{R+r}$����Դ���������Ϊ$\frac{{E}^{2}R}{��R+r��^{2}}$�����·���ĵĹ���Ϊ$\frac{{E}^{2}R}{��R+r��^{2}}$���ڲ����ĵĹ���Ϊ$\frac{{E}^{2}r}{��R+r��^{2}}$����Դ�Ĺ���Ч��Ϊ$\frac{R}{R+r}$��100%���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
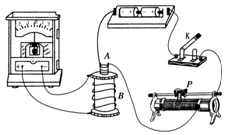 �ڡ�̽����Ÿ�Ӧ�IJ�����������ʵ���У��ֽ�����顢����������������о����ȦA����ȦB�������������K����ͼ��ʾ���ӣ������K�պ�˲�䣬������ָ����ƫ��˵��B��Ȧ�����˸�Ӧ�������������K�Ͽ�˲�䣬������ָ��ᣨ��ᡱ���ᡱ��ƫת�������K�պϺ�Ҫʹ��������ָ����ƫ���ɲ�ȡ�IJ���Ϊ�����������Ļ�ƬP���һ�����
�ڡ�̽����Ÿ�Ӧ�IJ�����������ʵ���У��ֽ�����顢����������������о����ȦA����ȦB�������������K����ͼ��ʾ���ӣ������K�պ�˲�䣬������ָ����ƫ��˵��B��Ȧ�����˸�Ӧ�������������K�Ͽ�˲�䣬������ָ��ᣨ��ᡱ���ᡱ��ƫת�������K�պϺ�Ҫʹ��������ָ����ƫ���ɲ�ȡ�IJ���Ϊ�����������Ļ�ƬP���һ������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
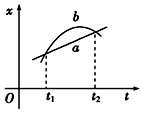
| A�� | ��t1ʱ�̣�a��b�������� | |
| B�� | ��t2ʱ�̣�a��b�����˶�������ͬ | |
| C�� | ��t1��t2���ʱ���ڣ�b���������ȼ�С������ | |
| D�� | ��t1��t2���ʱ���ڣ�b��������һֱ��a���Ĵ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
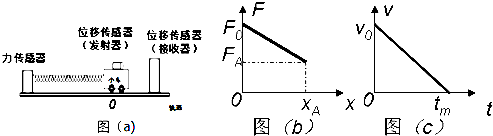
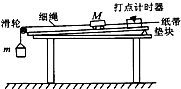 ��ͼ��ʾ���ڡ�̽�����ٶ�a����F������M�Ĺ�ϵ��ʵ���У�ijͬѧ���֣����˶���ֱ�Ӳ��С���������������룩���ܵ�ϸ�������ڲ�������һ�����ѣ�����С��������MԶ�������������mʱ��ѡ���Զ���ڡ���ԶС�ڡ��������Խ��Ƶ���ΪС�����ܵ�ϸ�������Ĵ�СF=mg��
��ͼ��ʾ���ڡ�̽�����ٶ�a����F������M�Ĺ�ϵ��ʵ���У�ijͬѧ���֣����˶���ֱ�Ӳ��С���������������룩���ܵ�ϸ�������ڲ�������һ�����ѣ�����С��������MԶ�������������mʱ��ѡ���Զ���ڡ���ԶС�ڡ��������Խ��Ƶ���ΪС�����ܵ�ϸ�������Ĵ�СF=mg���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com