
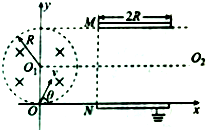
 ��ͼ��ʾ��һ�뾶ΪR��Բ��ʾһ��������Ľ��棬Բ������Ϊ��0��R���������������ڼ�һ����ֱֽ������Ÿ�Ӧǿ��ΪB����ǿ�ų����ڴų��Ҳ���һƽ����x����õ�ƽ�н�����M��N��������Ͱ峤��Ϊ2R�����н�����N��x���غ��ҽӵأ�һ����Ϊm�������Ϊ-q�Ĵ������ӣ�������ԭ��O��ֽ��������ͬ�����ʣ��ز�ͬ�ķ��������һ��������ų�ʱ���ӵķ���ƽ����x�ᣬ������������
��ͼ��ʾ��һ�뾶ΪR��Բ��ʾһ��������Ľ��棬Բ������Ϊ��0��R���������������ڼ�һ����ֱֽ������Ÿ�Ӧǿ��ΪB����ǿ�ų����ڴų��Ҳ���һƽ����x����õ�ƽ�н�����M��N��������Ͱ峤��Ϊ2R�����н�����N��x���غ��ҽӵأ�һ����Ϊm�������Ϊ-q�Ĵ������ӣ�������ԭ��O��ֽ��������ͬ�����ʣ��ز�ͬ�ķ��������һ��������ų�ʱ���ӵķ���ƽ����x�ᣬ���������������� ������Բ�δų�������˶����������DZȽϸ��ӵ�������ؼ�������ų�ʱ���ӵķ���ƽ����x�ᣬ�Ӵ˵���������ҵ�����Կ�ף�
��1��������Բ�ཻ�ļ��ι��ɣ�����ȷ�����ӵĹ���뾶����Բ�δų�����İ뾶�������������ṩ�����Ӷ�������ӵ��ٶȣ�
��2����60����������ӣ������뾶ΪR�Ļ����Բ�α߽�������ɼ��ι�ϵ�����������Ҳ�����ѣ�
��3������ƽ�������ֱ����糡��Ҫ������糡����ֻ�ܴ��ϡ��°�ı�Ե�������ȥ���ǣ�������ƽ�Ĺ��ɺ�ţ�ٵڶ����ɣ�����������ٶȴӶ������M��������ƣ�
���  �⣺��1����������x�������Ǧ�����Բ�δų����˶��켣��ͼ��ʾ
�⣺��1����������x�������Ǧ�����Բ�δų����˶��켣��ͼ��ʾ
�ɼ��ι�ϵ��֪���켣Բ��O'�������P��O'��O��O1�������Σ���������ڴų����˶��Ĺ켣�뾶ΪR��
��ţ�ٵڶ����ɿɵã�
$qvB=m\frac{v^2}{R}$
��ã�$v=\frac{qBR}{m}$
��2���������ڴų����˶���ʱ��Ϊt����
$t=\frac{��R}{v}=\frac{��m}{3qB}$��
��ͼ��ʾ������ų���λ������Ϊ��
$x=Rsin��=\frac{{\sqrt{3}}}{2}R$
$y=R��1-cos�ȣ�=\frac{1}{2}R$
������ų���λ������Ϊ$��\frac{{\sqrt{3}}}{2}R��\frac{1}{2}R��$
��3����������������˶���ʱ��Ϊt����
$t=\frac{2R}{v}=\frac{2m}{qB}$
�����ӴӰ��Ҳ����ʱ����λ��Ϊd���������糡ǿ��ΪE����
$d=\frac{1}{2}a{t^2}$
qE=ma
�ʽ�ã�$E=\frac{{q{B^2}d}}{2m}$
�����Ӵ�N���Ҳ��Ե���ʱ��
${d_1}=\frac{1}{2}R$��
��${U_{NM1}}={E_1}•2R=\frac{{q{B^2}{R^2}}}{2m}$
��M��ĵ��� ${��_{M1}}=-\frac{{q{B^2}{R^2}}}{2m}$
�����Ӵ�M����Ҳ��Ե���ʱ
${d_2}=\frac{3}{2}R$
��${U_{M2N}}={E_2}•2R=\frac{{3q{B^2}{R^2}}}{2m}$
��M��ĵ��� ${��_{M2}}=\frac{{3q{B^2}{R^2}}}{2m}$
���������ܹ���ƽ�а���Ҷ������M��ĵ��Ʒ�ΧΪ$-\frac{{q{B^2}{R^2}}}{2m}��{��_M}��\frac{{3q{B^2}{R^2}}}{2m}$
�𣺣�1�����������ڴų����˶����ٶȴ�СΪ$\frac{qBv}{m}$��
��2����O������ų�ʱ���ٶ�ǡ��x��ɦ�=60��ǵĴ�����������ų�ʱ��λ������Ϊ$��\frac{\sqrt{3}}{2}R��\frac{1}{2}R��$��
��3����ʹ�ڣ�2�����е������ܹ���ƽ�а�����������M�ĵ��Ʒ�Χ���$-\frac{q{B}^{2}{R}^{2}}{2m}��{��}_{M}��\frac{3q{B}^{2}{R}^{2}}{2m}$��
���� ����Ŀ�������������Բ�δų��������˶�����ƽ����x�ᴹֱ������ǿ�糡���ҵ�����Բ���˶��İ뾶�ǹؼ��������漰����ѧ���ι�ϵ--���Ρ�Բ������ȶ�����ѧ���ѵ㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
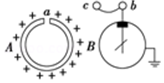 ��ͼ��ʾ���������A�������磬���Ϸ���һС��a�������B�Ľ�����b�õ��������С��c���������²�����������������ȷ���ǣ�������
��ͼ��ʾ���������A�������磬���Ϸ���һС��a�������B�Ľ�����b�õ��������С��c���������²�����������������ȷ���ǣ�������| A�� | ��c�ƽ�A��������A�Ӵ���B���ſ�һ���Ƕ� | |
| B�� | ��c��A�����Ӵ����ƿ�A��B�����ſ�һ���Ƕ� | |
| C�� | ��c��A�ڱ���Ӵ�ʱ��B�����ſ��Ƕ� | |
| D�� | ��c�ӵ����Ͻ��£�Ȼ���þ�Եϸ�����Ŵ�A��С������A�ڣ��������ڱڽӴ����������ǻ����b�Ӵ���B���ſ�һ���Ƕ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��������е��ɵĵ糡ǿ�ȹ�ʽE=k$\frac{Q}{{r}^{2}}$��֪���糡��ij��ĵ糡ǿ���볡Դ�������������й� | |
| B�� | ���ݵ��Ʋ�Ķ���ʽUAB=$\frac{{W}_{AB}}{q}$��֪���������Ϊ1C������ɣ���A���ƶ���B��˷��糡������Ϊ1J����A��B�����ĵ��Ʋ�Ϊ | |
| C�� | ���ݵ糡ǿ�ȵĶ���ʽE=$\frac{F}{q}$��֪���糡��ij��ĵ糡ǿ������̽��������ĵ�����ɷ��� | |
| D�� | ���ݵ��ݵĶ���ʽC=$\frac{Q}{U}$��֪���������ĵ���������������������ȣ����������ĵ�ѹ�ɷ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
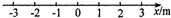 ��ͼ��ʾ���������������������������ֲ�ͬ�Ľ��ʣ�ԭ�㴦��һ��Դ����Դ������������������д�����P��Q������ֱ�ΪxP=-2m��xQ=2m�������ʵ㣮����P��Q���ʵ�������������˵����ȷ���ǣ�������
��ͼ��ʾ���������������������������ֲ�ͬ�Ľ��ʣ�ԭ�㴦��һ��Դ����Դ������������������д�����P��Q������ֱ�ΪxP=-2m��xQ=2m�������ʵ㣮����P��Q���ʵ�������������˵����ȷ���ǣ�������| A�� | ���ʵ�һ��ͬʱ���� | |
| B�� | ���ʵ����Ƶ��һ����ͬ | |
| C�� | P�ʵ㵽�ﲨ��ʱ��Q�ʵ�Ҳһ�����ﲨ�� | |
| D�� | ���ʵ������һ����ͬ | |
| E�� | P��Q��������ʵ�ֱ�������γ��ֲ����ʱ������ͬ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
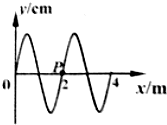 ����Ϊ2.0s�ļ�г�Შ��x�ᴫ�����ò���ijʱ�̵IJ���ͼ����ͼ��ʾ����ʱ�ʵ�P����y���������˶�����ò���������
����Ϊ2.0s�ļ�г�Შ��x�ᴫ�����ò���ijʱ�̵IJ���ͼ����ͼ��ʾ����ʱ�ʵ�P����y���������˶�����ò���������| A�� | ����Ϊ2m | |
| B�� | ����v=2m/s | |
| C�� | ��x�Ḻ���� | |
| D�� | �ʵ�P��1sʱ�����ز��Ĵ�������ǰ��2m |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
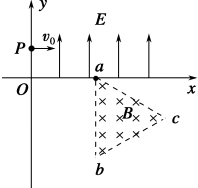 ��ͼ��ʾ��ƽ��ֱ������ϵxOy���ڵ�I��������ƽ����y�����ǿ�糡��������y���������ڵڢ�������������abc����������ǿ�ų�������ֱ��xOyƽ������������α߳�ΪL����ab����y��ƽ�У�һ����Ϊm�������Ϊq�����ӣ���y���ϵ�p��0��h���㣬�Դ�СΪv0���ٶ���x������������糡��ͨ���糡���x���ϵ�a��2h��0������˵ڢ����ޣ��־����ų���y���ϵ�ij����˵ڢ����ޣ����ٶ���y�Ḻ�����45��ǣ������������ܵ���������
��ͼ��ʾ��ƽ��ֱ������ϵxOy���ڵ�I��������ƽ����y�����ǿ�糡��������y���������ڵڢ�������������abc����������ǿ�ų�������ֱ��xOyƽ������������α߳�ΪL����ab����y��ƽ�У�һ����Ϊm�������Ϊq�����ӣ���y���ϵ�p��0��h���㣬�Դ�СΪv0���ٶ���x������������糡��ͨ���糡���x���ϵ�a��2h��0������˵ڢ����ޣ��־����ų���y���ϵ�ij����˵ڢ����ޣ����ٶ���y�Ḻ�����45��ǣ������������ܵ����������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
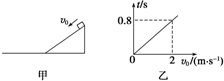 ��ͼ����ʾ����ͬ�ֲ����Ƴɵ����Ϊ30���б��ͳ�ˮƽ�棬б���ˮƽ��֮���ɹ⻬Բ�����ӣ�б�泤Ϊ2.4m�ҹ̶���һС����б�涥������б�����µij��ٶ�v0��ʼ�����»�����v0=2m/sʱ������0.8s��С���ͣ��б���ϣ���θı�v0�Ĵ�С����¼��С���ӿ�ʼ�˶�������ͣ�µ�ʱ��t������t-v0ͼ����ͼ����ʾ��gȡ10m/s2��������
��ͼ����ʾ����ͬ�ֲ����Ƴɵ����Ϊ30���б��ͳ�ˮƽ�棬б���ˮƽ��֮���ɹ⻬Բ�����ӣ�б�泤Ϊ2.4m�ҹ̶���һС����б�涥������б�����µij��ٶ�v0��ʼ�����»�����v0=2m/sʱ������0.8s��С���ͣ��б���ϣ���θı�v0�Ĵ�С����¼��С���ӿ�ʼ�˶�������ͣ�µ�ʱ��t������t-v0ͼ����ͼ����ʾ��gȡ10m/s2��������| A�� | С�������ֲ��ϼ�Ķ�Ħ������Ϊ0.25 | |
| B�� | С�������ֲ��ϼ�Ķ�Ħ������Ϊ$\frac{\sqrt{3}}{2}$ | |
| C�� | ��С�����ٶ�Ϊ1 m/s�������ͼ���֪С����˶�ʱ��Ϊ0.4 s | |
| D�� | ��С�����ٶ�Ϊ4 m/s�������ͼ���֪С����˶�ʱ��Ϊ1.6 s |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
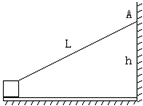 ��ͼ����Ȳ��Ƶij�ľ�����ˮƽ���ϣ������Ҷ˽�����ֱǽ�ڣ�ľ�������֮��Ħ��ϵ����1=0.25��ľ������M=0.4kg��������һ����Ϊm=0.3kg��С���壬��ľ���Ħ��ϵ����2=$\frac{1}{3}$����С�����ó�ΪL=1mϸ��ϵ��ǽ��A�㣬A��߶�h=0.6m����ˮƽ��F=6.4N��ľ�壬ʹ��Ӿ�ֹ��ʼ�˶�����ʱϸ�����Ž��ģ����ʾ��ʱ��С�����뿪ľ���Ҷˣ�
��ͼ����Ȳ��Ƶij�ľ�����ˮƽ���ϣ������Ҷ˽�����ֱǽ�ڣ�ľ�������֮��Ħ��ϵ����1=0.25��ľ������M=0.4kg��������һ����Ϊm=0.3kg��С���壬��ľ���Ħ��ϵ����2=$\frac{1}{3}$����С�����ó�ΪL=1mϸ��ϵ��ǽ��A�㣬A��߶�h=0.6m����ˮƽ��F=6.4N��ľ�壬ʹ��Ӿ�ֹ��ʼ�˶�����ʱϸ�����Ž��ģ����ʾ��ʱ��С�����뿪ľ���Ҷˣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com