
| A. | $\frac{g}{4}$ | B. | $\frac{g}{2}$ | C. | g | D. | 无法确定 |
分析 根据地球表面重力与万有引力相等,人造卫星由万有引力提供圆周运动向心力,同此列式分析即可.
解答 解:在地球表面重力与有引力相等有:
$G\frac{mM}{{R}^{2}}=mg$
可得:GM=gR2
离地面高度为R的卫星轨道半径r=2R,圆周运动向心力由万有引力提供,故有:
$G\frac{mM}{(2R)^{2}}=ma$
可得卫星的向心加速度为:a=$\frac{GM}{4{R}^{2}}=\frac{g{R}^{2}}{4{R}^{2}}=\frac{g}{4}$
故选:A.
点评 解决本题的关键是抓住万有引力与地球表面重力相等,万有引力提供卫星圆周运动向心力,用好黄金代换式是关键.


科目:高中物理 来源: 题型:解答题
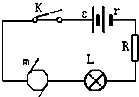 如图所示,已知电源电动势E=20V,内阻r=1Ω,当接入固定电阻R=4Ω时,电路中标有“3V 6W”的灯泡L正常工作和内阻r′=0.5Ω的小型直流电动机恰能正常工作,
如图所示,已知电源电动势E=20V,内阻r=1Ω,当接入固定电阻R=4Ω时,电路中标有“3V 6W”的灯泡L正常工作和内阻r′=0.5Ω的小型直流电动机恰能正常工作,查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 匀强电场中有a、b、c三点.在以它们为顶点的三角形中,∠a=30°、∠c=90°,电场方向与三角形所在平面平行.已知a、b和c点的电势分别为(2-$\sqrt{3}$)V、(2+$\sqrt{3}$)V和2V.该三角形的外接圆上最低、最高电势分别为( )
匀强电场中有a、b、c三点.在以它们为顶点的三角形中,∠a=30°、∠c=90°,电场方向与三角形所在平面平行.已知a、b和c点的电势分别为(2-$\sqrt{3}$)V、(2+$\sqrt{3}$)V和2V.该三角形的外接圆上最低、最高电势分别为( )| A. | (2-$\sqrt{3}$)V、(2+$\sqrt{3}$)V | B. | 0 V、4 V | C. | (2-$\sqrt{3}$)V、(2+$\frac{4\sqrt{3}}{3}$)V | D. | 0 V、$\sqrt{3}$V |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,在一个水平向右匀加速直线运动的质量为M的车厢里,用一个定滑轮通过绳子悬挂两个物体,物体的质量分别为m1、m2.已知m1<m2,m2静止在车厢的地板上,m1向左偏离竖直方向θ角.这时,作用在m2上的摩擦力大小是多少?车厢的地板对m2的支持力为多少?
如图所示,在一个水平向右匀加速直线运动的质量为M的车厢里,用一个定滑轮通过绳子悬挂两个物体,物体的质量分别为m1、m2.已知m1<m2,m2静止在车厢的地板上,m1向左偏离竖直方向θ角.这时,作用在m2上的摩擦力大小是多少?车厢的地板对m2的支持力为多少?查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,小球在斜面顶点A处以v0=10米/秒的水平速度抛出,求小球抛出后经过多长时间离斜面的距离最大?若着地点为斜面的末端B,则斜面的长是多少?
如图所示,小球在斜面顶点A处以v0=10米/秒的水平速度抛出,求小球抛出后经过多长时间离斜面的距离最大?若着地点为斜面的末端B,则斜面的长是多少?查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 在抛球过程中人对小球做的功是$\frac{1}{2}$mv02 | |
| B. | 下落过程中重力对物体做的功是mgh | |
| C. | 物体下落地时的速度大小为v0+$\sqrt{2gh}$ | |
| D. | 物体落地时的速度大小为$\sqrt{{V_0}^2+2gh}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 若两球质量相等,碰后以某一相等速率同向而行 | |
| B. | 若两球质量相等,碰后以某一相等速率互相分开 | |
| C. | 若两球质量不同,碰后以某一相等速率互相分开 | |
| D. | 若两球质量不同,碰后以某一相等速率同向而行 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com