

分析 (1)当木板和物块刚要发生相对运动时,两者间的静摩擦力达到最大值,分别整体和物块运用牛顿第二定律可求得F的最小值.
(2)根据牛顿第二定律研究物块和木板的加速度,由运动学公式分段求出木板和物块的速度,即可画出v-t图象.
(3)物块在木板上留下的痕迹的长度等于物块与木板的相对位移大小,由位移公式求解.
解答 解:(1)把物块和木板看作整体,由牛顿第二定律得:F=(m1+m2)a
对物块,物块与木板将要相对滑动时有 μ1m1g=m1a
联立解得 F=μ1(m1+m2)g=8N
(2)物块在0~2s内做匀加速直线运动,由牛顿第二定律有:μ1m1g=m1a1
解得 a1=2m/s2;
2s末物块的速度为 v1=a1t1=2×2=4(m/s)
木板在0~1s内做匀加速直线运动,由牛顿第二定律有:F1-μ1m1g=m2a2
解得 a2=4m/s2;
1s末木板的速度 v1′=a2t2=4×1=4(m/s)
在1~2s内 F2=μ1m1g,木板做匀速运动,速度为4m/s
如果物块和木板一起减速运动,共同的加速度为 ${a_共}=\frac{{({m_1}+{m_2})g{μ_2}}}{{({m_1}+{m_2})}}=g{μ_2}$
m1的合力m1gμ2>fm=m1gμ1
所以物块和木板相对滑动
2s后物块做匀减速直线运动,由牛顿第二定律有:-μ1m1g=m1a3
得:a3=-2m/s2;
速度从4m/s减至零的时间 t3=$\frac{0-{v}_{1}}{{a}_{3}}$=$\frac{0-4}{-2}$=2(s)
木板做匀减速直线运动有:-μ2(m1+m2)g+μ1m1g=m2a4
得:a4=-$\frac{8}{3}$m/s2;
速度从4m/s减至零的时间 t4=$\frac{0-{v}_{1}′}{{a}_{4}}$=$\frac{-4}{-\frac{8}{3}}$=1.5(s)
二者在整个运动过程的v-t图象如图所示(实线是木板的v-t图象,虚线是物块的v-t图象)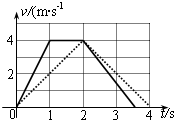
(3)0~2s内物块相对木板向左运动 $△{x_1}=\frac{1}{2}{a_1}t_1^2+({a_1}{t_1})t{\;}_2-\frac{1}{2}{a_2}{({t_1}+{t_2})^2}$
2-4s内物块相对木板向右运动 $△{x_2}=\frac{{-{{({a_1}{t_1})}^2}}}{{2{a_4}}}-\frac{{-{{({a_1}{t_1})}^2}}}{{2{a_3}}}$
△x1>△x2
所以0~4s内物块在木板痕迹的长度为△x=△x1=2m
答:(1)为使木板和物块发生相对运动,拉力F至少应为8N.
(2)如图所示.
(3)0~4s内物块在木板上留下的痕迹的长度为2m.
点评 根据物体受力情况判断物体的运动情况,并根据牛顿第二定律及匀变速直线运动的基本公式解题的典型例题,要注意题中F是个变力,在1s后发生了改变,所以加速度也要发生变化.求位移差时也可根据速度时间图象与时间轴所围成的面积表示位移去求解.


科目:高中物理 来源: 题型:选择题
| A. | 探究加速度与力和质量关系的实验运用了控制变量法 | |
| B. | 电学中电阻、电场强度和电势的定义都运用了比值法 | |
| C. | 力学中将物体看成质点运用了理想化模型法 | |
| D. | 当物体的运动时间△t趋近于0时,△t时间内的平均速度可看成瞬时速度运用了等效替代法 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 全部正确 | B. | ①式错误 | ||
| C. | ②式错误 | D. | ③式以后的逻辑错误 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
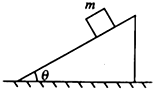 如图所示,粗糙的水平地面上有一质量为M、倾角为θ的斜劈,斜劈上有一质量为m的小物块正沿斜面下滑,小物块与斜面之间无摩擦,斜劈始终保持静止,则在小物块下滑的过程中斜劈受到水平地面的摩擦力和支持力大小分别是( )
如图所示,粗糙的水平地面上有一质量为M、倾角为θ的斜劈,斜劈上有一质量为m的小物块正沿斜面下滑,小物块与斜面之间无摩擦,斜劈始终保持静止,则在小物块下滑的过程中斜劈受到水平地面的摩擦力和支持力大小分别是( )| A. | 0;(M+m)g | B. | 0;Mg+mgcos2θ | ||
| C. | mgsinθcosθ;Mg+mgcos2θ | D. | mgtanθ;Mg+mgcosθ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
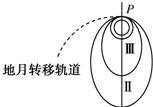 某探月卫星沿地月轨道直奔月球,在距月球表面的P点进行第一次变轨后被月球捕获,先进入椭圆轨道Ⅰ绕月飞行,如图所示.之后,卫星在P点又经过两次变轨,最后在距月球表面200km的圆形轨道Ⅲ上绕月球做匀速圆周运动.对此,下列说法错误的是( )
某探月卫星沿地月轨道直奔月球,在距月球表面的P点进行第一次变轨后被月球捕获,先进入椭圆轨道Ⅰ绕月飞行,如图所示.之后,卫星在P点又经过两次变轨,最后在距月球表面200km的圆形轨道Ⅲ上绕月球做匀速圆周运动.对此,下列说法错误的是( )| A. | 卫星在轨道Ⅲ上运动的速度小于月球的第一宇宙速度 | |
| B. | 卫星在轨道Ⅲ上运动周期比在轨道Ⅰ上短 | |
| C. | 卫星在轨道Ⅲ上运动的加速度大于沿轨道Ⅰ运动到P点时的加速度 | |
| D. | Ⅰ、Ⅱ、Ⅲ三种轨道运行相比较,卫星在轨道Ⅲ上运行的机械能最大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com