
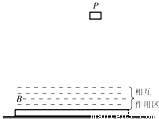
 质量M=10kg的B板上表面上方,存在一定厚度的相互作用区域,如图中划虚线的部分,当质量m=1kg的物块P进入相互作用区时,B便有竖直向上的恒力f作用于P,f=kmg,k=51,f对P的作用使P刚好不与B的上表面接触;在水平方向,P、B之间没有相互作用力.已知物块P开始自由下落的时刻,B板向右运动的速度为v0=10m/s.P从开始下落到刚到达相互作用区所经历的时间为T0=2.0s.设B板足够长,B板与水平面间的动摩擦因数μ=0.02,为保证物块P总能落入B板上方的相互作用区,问:当B刚好停止运动时,P已经回到过初始位置几次?(g=9.8m/s2)
质量M=10kg的B板上表面上方,存在一定厚度的相互作用区域,如图中划虚线的部分,当质量m=1kg的物块P进入相互作用区时,B便有竖直向上的恒力f作用于P,f=kmg,k=51,f对P的作用使P刚好不与B的上表面接触;在水平方向,P、B之间没有相互作用力.已知物块P开始自由下落的时刻,B板向右运动的速度为v0=10m/s.P从开始下落到刚到达相互作用区所经历的时间为T0=2.0s.设B板足够长,B板与水平面间的动摩擦因数μ=0.02,为保证物块P总能落入B板上方的相互作用区,问:当B刚好停止运动时,P已经回到过初始位置几次?(g=9.8m/s2)



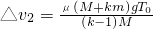

 为整数,故有n0=11,即当B开始停止运动的那一时刻,P已经回到过初始位置11次
为整数,故有n0=11,即当B开始停止运动的那一时刻,P已经回到过初始位置11次 

科目:高中物理 来源: 题型:
 (2011?荆州一模)用图所示的水平传送带AB和斜面BC将货物运送到斜面的顶端.传送带AB的长度L=11m,上表面保持匀速向右运行,运行的速度v=12m/s.传送带B端靠近倾角θ=37°的斜面底端,斜面底端与传送带的B端之间有一段长度可以不计的小圆弧.在A、C处各有一个机器人,A处机器人每隔△t=1.0s将一个质量m=10kg的货物箱(可视为质点)轻放在传送带A端,货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零,C点处机器人立刻将货物箱搬走.已知斜面BC的长度s=5.0m,传送带与货物箱之间的动摩擦因数μ0=0.55,货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的
(2011?荆州一模)用图所示的水平传送带AB和斜面BC将货物运送到斜面的顶端.传送带AB的长度L=11m,上表面保持匀速向右运行,运行的速度v=12m/s.传送带B端靠近倾角θ=37°的斜面底端,斜面底端与传送带的B端之间有一段长度可以不计的小圆弧.在A、C处各有一个机器人,A处机器人每隔△t=1.0s将一个质量m=10kg的货物箱(可视为质点)轻放在传送带A端,货物箱经传送带和斜面后到达斜面顶端的C点时速度恰好为零,C点处机器人立刻将货物箱搬走.已知斜面BC的长度s=5.0m,传送带与货物箱之间的动摩擦因数μ0=0.55,货物箱由传送带的右端到斜面底端的过程中速度大小损失原来的| 1 | 11 |
查看答案和解析>>
科目:高中物理 来源: 题型:
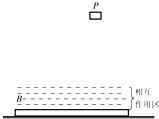
 质量M=10kg的B板上表面上方,存在一定厚度的相互作用区域,如图中划虚线的部分,当质量m=1kg的物块P进入相互作用区时,B便有竖直向上的恒力f作用于P,f=kmg,k=51,f对P的作用使P刚好不与B的上表面接触;在水平方向,P、B之间没有相互作用力.已知物块P开始自由下落的时刻,B板向右运动的速度为v0=10m/s.P从开始下落到刚到达相互作用区所经历的时间为T0=2.0s.设B板足够长,B板与水平面间的动摩擦因数μ=0.02,为保证物块P总能落入B板上方的相互作用区,问:当B刚好停止运动时,P已经回到过初始位置几次?(g=9.8m/s2)
质量M=10kg的B板上表面上方,存在一定厚度的相互作用区域,如图中划虚线的部分,当质量m=1kg的物块P进入相互作用区时,B便有竖直向上的恒力f作用于P,f=kmg,k=51,f对P的作用使P刚好不与B的上表面接触;在水平方向,P、B之间没有相互作用力.已知物块P开始自由下落的时刻,B板向右运动的速度为v0=10m/s.P从开始下落到刚到达相互作用区所经历的时间为T0=2.0s.设B板足够长,B板与水平面间的动摩擦因数μ=0.02,为保证物块P总能落入B板上方的相互作用区,问:当B刚好停止运动时,P已经回到过初始位置几次?(g=9.8m/s2)查看答案和解析>>
科目:高中物理 来源:南通模拟 题型:问答题
查看答案和解析>>
科目:高中物理 来源:2007-2008学年江苏省南通市通州区高三(上)第一次调研物理试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com