
 ��ͼ��ʾ��һ����m=0.2kg�Ŀ���Ϊ�ʵ��С���飬��һ���ij��ٶȻ��ϳ�Ϊl=1m��ˮƽ���ʹ��Ҷ�A��С�����봫�ʹ���Ķ�Ħ��������=0.2�����ʹ������B��һ�⻬��Բ�������C������С�����ܴ�Ƥ���ϵ�B��ͨ��Բ�������C�����Բ������ڲ࣬����������ʧ��Բ������İ뾶R=0.4m��Բ������ĵ�D��һ��Ϊh=0.8m���ױ߳�Ϊx=2m�Ĺ⻬б��EFG��E�����ӣ���gȡ10m/s2��
��ͼ��ʾ��һ����m=0.2kg�Ŀ���Ϊ�ʵ��С���飬��һ���ij��ٶȻ��ϳ�Ϊl=1m��ˮƽ���ʹ��Ҷ�A��С�����봫�ʹ���Ķ�Ħ��������=0.2�����ʹ������B��һ�⻬��Բ�������C������С�����ܴ�Ƥ���ϵ�B��ͨ��Բ�������C�����Բ������ڲ࣬����������ʧ��Բ������İ뾶R=0.4m��Բ������ĵ�D��һ��Ϊh=0.8m���ױ߳�Ϊx=2m�Ĺ⻬б��EFG��E�����ӣ���gȡ10m/s2������ ��1���Ի����A��B�Ĺ���Ϊ�о�����Ӧ�ö��ܶ���������������ٶȣ���C��Ӧ��ţ�ٵڶ����ɿ���C����ٶȣ���ΪB���ٶȣ����Եõ����ٶȣ�
��2����һֱ���ٵ�C�ٶ������ţ�ٵڶ����ɿɵü��ٶȣ����˶�ѧ����ĩ�ٶȣ�����ţ�ٵڶ����ɿɵ����ѹ����
��3����D��F��ƽ���˶�����ƽ���ɿ���D���ٶȣ��ɶ��ܶ�������C����ٶȣ����ٶ�ΪƤ���ٶȵ����ֵ��
��� �⣺��1�������A��B���̣����ݶ��ܶ��ɣ��У�$-��mgl=\frac{1}{2}m{{v}_{1}}^{2}-\frac{1}{2}m{{v}_{0}}^{2}$��
��C�㣬�����ṩ���������У�$mg=m\frac{{{v}_{1}}^{2}}{R}$��
������ã�${v}_{0}=\sqrt{{{v}_{1}}^{2}+2��mgl}$=$\sqrt{10��0.4+2��0.2��10��1}=2\sqrt{2}m/s$��
��2�����һֱ���٣����ٶȣ�a=��g=2m/s2��
�����ٶ�λ�ƹ�ʽ���У�${{v}_{2}}^{2}-{{v}_{0}}^{2}=2al$��
��ã�${v}_{2}=\sqrt{{{v}_{1}}^{2}+2��gl}=\sqrt{8+2��2��1}=2\sqrt{3}m/s$��
��C�㣬�����ṩ���������ʣ�$N+mg=m\frac{{{v}_{2}}^{2}}{R}$��
��ã�$N=m\frac{{{v}_{2}}^{2}}{R}-mg=0.2��\frac{12}{0.4}-0.2��10=4N$��
��D�㣬��ţ�ٵڶ����ɣ����У�$N��-mg=m\frac{{v}_{D}^{2}}{R}$��
����C��D�����ݶ��ܶ��������У�$\frac{1}{2}m{v}_{D}^{2}-\frac{1}{2}m{v}_{C}^{2}=2mgR$
��ã�N��=16N��
��ţ�ٵ������ɣ����ѹ��Ϊ16N��
��3����D��F��ƽ���˶����ʣ�
x=vDt��
$h=\frac{1}{2}g{t}^{2}$��
��ã�${v}_{D}=x\sqrt{\frac{g}{2h}}=2��\sqrt{\frac{10}{2��0.8}}=5m/s$��
��C��D���ݶ��ܶ�����$mg2R=\frac{1}{2}m{{v}_{D}}^{2}-\frac{1}{2}m{{v}_{C}}^{2}$
��ã�vC=3m/s��
�ʴ��ʹ����ٶȷ�Χ��$2\sqrt{2}m/s��v��3m/s$��
�𣺣�1����Ƥ����ֹ��ҪʹС�����ܻ���Բ�������Բ�˶���С���黬��Ƥ���Ҷ�ʱ����С�ٶ�v0�Ĵ�СΪ$2\sqrt{2}m/s$��
��2����Ƥ������ʱ�뷽��ת����Ƥ���ٶȿ�ȡ��ͬ��ֵ��С�����Եڣ�1�����е�v0����Ƥ���Ҷˣ�С�����˶���Բ����D��ʱ�����С����֧���������ֵ16N��
��3����Ƥ��������ʱ�뷽��ת����Ƥ���ٶȿ�ȡ��ͬ��ֵ��С�����Եڣ�1�����е�v0����Ƥ���Ҷˣ�ҪʹС��������б��EF�ϣ�Ƥ���ٶ�v��ȡֵ��Χ$2\sqrt{2}m/s��v��3m/s$��
���� ����Ҫϸ�·���������˶�������ۺ��˶�ѧ�����ܶ��ɣ�Բ���˶��ȣ�����Ҫ��ϸߣ���һ���Ѷ���Խϴ����Ŀ��


 �����������һ��һ��ϵ�д�
�����������һ��һ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
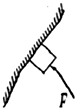
| A�� | ľ�������������� | B�� | ľ�����ĸ������� | ||
| C�� | ����F������ľ����ܻ��� | D�� | ľ������Ħ������F����������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ����ʾQ1��Q2Ϊ�������̶��ĵ��ɣ�����Q1Ϊ�����ɣ����������ߵ��ӳ�������a��b���㣮����һ������q������δ֪����һ���ij��ٶ���ֱ�ߴ�b�㿪ʼ��a����Զ���˶���������ֻ�ܵ糡�����ã���q�˶����ٶ�ͼ����ͼ����ʾ��������
��ͼ����ʾQ1��Q2Ϊ�������̶��ĵ��ɣ�����Q1Ϊ�����ɣ����������ߵ��ӳ�������a��b���㣮����һ������q������δ֪����һ���ij��ٶ���ֱ�ߴ�b�㿪ʼ��a����Զ���˶���������ֻ�ܵ糡�����ã���q�˶����ٶ�ͼ����ͼ����ʾ��������| A�� | Q2�ض��Ǹ���� | |
| B�� | ����ȷ�������ɵĴ������� | |
| C�� | Q2�ĵ�����ض�����Q1�ĵ���� | |
| D�� | ��b�㾭a����Զ���˶��Ĺ����е��Q���ܵĵ糡��һֱ��С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 �������Ϊ��С�������Ĺ��ݵ������и߶�610m����Ŀǰ��������ߵĵ��ӹ۹������ס������οͳ�ͬһ���۹�������ع۹��������˶����Դ˹��̣�����˵����ȷ���ǣ�������
�������Ϊ��С�������Ĺ��ݵ������и߶�610m����Ŀǰ��������ߵĵ��ӹ۹������ס������οͳ�ͬһ���۹�������ع۹��������˶����Դ˹��̣�����˵����ȷ���ǣ�������| A�� | �ס��ҿ��������ϵ��˺ͳ�Զ���Լ���ȥ�����Թ۹���Ϊ�ο�ϵ | |
| B�� | �ס��ҿ��������ϵ��˺ͳ�Զ���Լ���ȥ�����Ե���Ϊ�ο�ϵ | |
| C�� | ������û�������Ե���Ϊ�ο�ϵ | |
| D�� | ������û�������Թ۹���Ϊ�ο�ϵ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
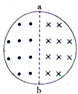 ��ͼ��ʾ����ͼ�οռ������ڴ��ڹ���ֱ��ab�Գơ������෴��������ǿ�ų������ų��ĴŸ�Ӧǿ�ȴ�С��ȣ�һ���������Ƴɵ�Բ���պ���ų��߽��غϣ�����˵��������ǣ�������
��ͼ��ʾ����ͼ�οռ������ڴ��ڹ���ֱ��ab�Գơ������෴��������ǿ�ų������ų��ĴŸ�Ӧǿ�ȴ�С��ȣ�һ���������Ƴɵ�Բ���պ���ų��߽��غϣ�����˵��������ǣ�������| A�� | ��ʹԲ������ƽ������Ӧ����������ʱ�뷽�����˳ʱ�뷽�� | |
| B�� | ��ʹԲ����ֱ����ƽ������Բ������Ӧ���� | |
| C�� | ��Բ����abΪ��ת����a��ĵ���һ������b��ĵ��� | |
| D�� | ��Բ����abΪ��ת����b��ĵ���һ������a��ĵ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ���ô�ϸ��ͬ��ͭ˿���ɱ߳��ֱ�ΪL��2L����ֻ�պ��������߿�a��b������ͬ���ٶȴӴŸ�Ӧǿ��ΪB����ǿ�ų����������ٵ������ų��⣬�������Ի����Ĺ��ֱ�ΪWa��Wb����Wa��WbΪ��������
��ͼ��ʾ���ô�ϸ��ͬ��ͭ˿���ɱ߳��ֱ�ΪL��2L����ֻ�պ��������߿�a��b������ͬ���ٶȴӴŸ�Ӧǿ��ΪB����ǿ�ų����������ٵ������ų��⣬�������Ի����Ĺ��ֱ�ΪWa��Wb����Wa��WbΪ��������| A�� | 1��4 | B�� | 1��2 | C�� | 1��1 | D�� | ����ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ���û���������������ˮƽ����������ǰ�������������Ķ˵�A����F=300N��������Ļ�еЧ��Ϊ80%���������������Ħ����fΪ���
��ͼ��ʾ���û���������������ˮƽ����������ǰ�������������Ķ˵�A����F=300N��������Ļ�еЧ��Ϊ80%���������������Ħ����fΪ����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 һ��վ�ڵ����е����ؼ��������һ���˶�����W��ʾ������������ʱ���ؼƵ�ʾ����W1��W2�ֱ��ʾ�����Դ�СΪa�ļ��ٶȼ��������ͼ�������ʱ���ؼƵ�ʾ����������
һ��վ�ڵ����е����ؼ��������һ���˶�����W��ʾ������������ʱ���ؼƵ�ʾ����W1��W2�ֱ��ʾ�����Դ�СΪa�ļ��ٶȼ��������ͼ�������ʱ���ؼƵ�ʾ����������| A�� | W2��W��W1 | B�� | W1��W��W2 | C�� | W��W1=W2 | D�� | W��W1=W2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com