
 ��ͼ��ʾ���ռ�����һ����������ABCD�������Խ���BD�ָ������ֱ�������Σ�����������ABD�д�������ֱ���µ���ǿ�糡��������BCD�д����Ŵ�ֱֽ�����ǿ�ų���ͼ��δ��������һ����Ϊm�������Ϊq���������Ӵ�A��ˮƽ���ٶ�v0���������Ȼ��BD�е�P���뵽��ǿ�ų������պô�ֱBC�߷ɳ�����֪AB=2L��AD=L����ô��˵����ȷ���ǣ�������
��ͼ��ʾ���ռ�����һ����������ABCD�������Խ���BD�ָ������ֱ�������Σ�����������ABD�д�������ֱ���µ���ǿ�糡��������BCD�д����Ŵ�ֱֽ�����ǿ�ų���ͼ��δ��������һ����Ϊm�������Ϊq���������Ӵ�A��ˮƽ���ٶ�v0���������Ȼ��BD�е�P���뵽��ǿ�ų������պô�ֱBC�߷ɳ�����֪AB=2L��AD=L����ô��˵����ȷ���ǣ�������| A�� | ��ǿ�糡�ĵ糡ǿ�ȴ�СΪ$\frac{2{mv}_{0}^{2}}{qL}$ | |
| B�� | ����P����ٶ�Ϊv0��������v0��45�� | |
| C�� | ��ǿ�ų��ĴŸ�Ӧǿ�ȴ�СΪ$\frac{{mv}_{0}^{2}}{qL}$������ֱֽ������ | |
| D�� | ����ʹ���ӷ��ص��糡������ô��ǿ�ų��ĴŸ�Ӧǿ������Ҫ����$\frac{��\sqrt{2}+1��{mv}_{0}}{qL}$ |
���� �����ڵ糡��������ƽ���˶�����������ƽ���˶��ķ�λ�ƹ�ʽ��ʽ���糡ǿ�ȣ����ݷ��ٶȹ�ʽ��ʽ���ĩ�ٶȣ��ڴų���������Բ���˶��������ٽ�켣�����ţ�ٵڶ����ɺͼ��ι�ϵ�������ɣ�
��� �⣺A����A��P����������ƽ���˶������ݷ�λ�ƹ�ʽ���У�
x=L=v0t
y=$\frac{L}{2}$=$\frac{1}{2}\frac{qE}{m}{t}^{2}$
������ã�E=$\frac{m{v}_{0}^{2}}{qL}$
��A����
B������P����ٶ�ƫת������ֵ��λ��ƫת������ֵ��2����Ϊ��
$tan��=2tan��=2��\frac{y}{x}=1$
�ʦ�=45��
��P���ٶ��ٶ�Ϊ��v=$\sqrt{2}$v0
��B���� C�����Ӵ�A��ˮƽ���ٶ�v0���������Ȼ��BD�е�P���뵽��ǿ�ų������պô�ֱBC�߷ɳ��������켣����ͼ��ʾ��
C�����Ӵ�A��ˮƽ���ٶ�v0���������Ȼ��BD�е�P���뵽��ǿ�ų������պô�ֱBC�߷ɳ��������켣����ͼ��ʾ��
���ڴų��еĹ���뾶Ϊ��
R=$\frac{L}{cos45��}$=$\sqrt{2}$L
����R=$\frac{mv}{qB}$��v=$\sqrt{2}$v0����
B=$\frac{{mv}_{0}^{\;}}{qL}$
�����Ǵ�ֱ���ڣ�
��C����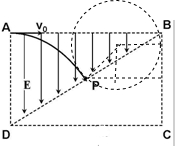 D����ʹ���ӷ��ص��糡�����ٽ�����켣��ͼ��ʾ��
D����ʹ���ӷ��ص��糡�����ٽ�����켣��ͼ��ʾ��
��ϼ��ι�ϵ���У�
Rsin45��+R=L
��ã�
R=$\frac{2L}{2+\sqrt{2}}$
����������Բ���˶�������ţ�ٵڶ����ɣ��У�
qvB=m$\frac{{v}^{2}}{R}$
��ã�B=$\frac{mv}{qR}=\frac{m��\sqrt{2}{v}_{0}}{q��\frac{2L}{2+\sqrt{2}}��}$=$\frac{��\sqrt{2}+1��{mv}_{0}}{qL}$��
��D��ȷ��
��ѡ��D��
���� ����ؼ�����ȷ���ӵ��˶����ɣ������˶��Ĺ켣����ϼ��ι�ϵ�õ�����뾶���ٽ��ţ�ٵڶ�������ʽ���������ѣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �ظ���ָ������ | B�� | ����Ϊ�� | C�� | ����ָ������ | D�� | �ظ���Ϊ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | mg | C�� | 3mg | D�� | 5mg |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ������ͬ��������������M��N����ͬ���ٶ��ش�ֱ�ڵ糡����������ƽ�а�����ǿ�糡�У�M�����������������룬N���¼����Ե�����룬����������ͬһ�㣨�������ƣ�����ͼ��ʾ����ӿ�ʼ���뵽�����ϼ���Ĺ����У�������
������ͬ��������������M��N����ͬ���ٶ��ش�ֱ�ڵ糡����������ƽ�а�����ǿ�糡�У�M�����������������룬N���¼����Ե�����룬����������ͬһ�㣨�������ƣ�����ͼ��ʾ����ӿ�ʼ���뵽�����ϼ���Ĺ����У�������| A�� | �����˶���ʱ��tN��tM | |
| B�� | ���ǵ����ܼ�����֮�ȡ�EM����EN=1��2 | |
| C�� | ���������ĵ����֮��qM��qN=1��2 | |
| D�� | ���ǵĶ�������֮�ȡ�EKM����EKN=2��1 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ�������뾶�ֱ�Ϊr1��r2�����������ȷֲ����ֱ�Ϊm1��m2������֮��ľ���Ϊr��������������������СΪ$G\frac{{m}_{1}{m}_{2}}{��{r}_{1}+r+{r}_{2}��^{2}}$��
��ͼ��ʾ�������뾶�ֱ�Ϊr1��r2�����������ȷֲ����ֱ�Ϊm1��m2������֮��ľ���Ϊr��������������������СΪ$G\frac{{m}_{1}{m}_{2}}{��{r}_{1}+r+{r}_{2}��^{2}}$���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��

| A�� | ����Ϊ4m | |
| B�� | ���ٴ�С1m/s | |
| C�� | t=2sʱ���ʵ�A�Ķ���Ϊ�� | |
| D�� | ��t=0��t=4s�ڣ��ʵ�Bͨ����·��Ϊ4m |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ����Ϊm��A������Ϊ2m��BС��֮��ϵһ���������Ƶĵ��ɣ����ڹ⻬��̨���ϣ�A����ǽ�ڣ���ͼ��ʾ�����ú���F��B������ѹ���ɣ��ﵽƽ��ʱ��ͻȻ������ȥ����˲�䣨������
����Ϊm��A������Ϊ2m��BС��֮��ϵһ���������Ƶĵ��ɣ����ڹ⻬��̨���ϣ�A����ǽ�ڣ���ͼ��ʾ�����ú���F��B������ѹ���ɣ��ﵽƽ��ʱ��ͻȻ������ȥ����˲�䣨������| A�� | A��ļ��ٶ�Ϊ�� | B�� | A��ļ��ٶ�Ϊ$\frac{F}{m}$ | ||
| C�� | B��ļ��ٶ�Ϊ$\frac{F}{2m}$ | D�� | B��ļ��ٶ�Ϊ$\frac{F}{m}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �������ĵ���$C=\frac{Q}{U}$ | B�� | ���ٶ�a=$\frac{F}{m}$ | ||
| C�� | �糡ǿ��E=$\frac{F}{q}$ | D�� | �Ÿ�Ӧǿ��B=$\frac{F}{IL}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com