
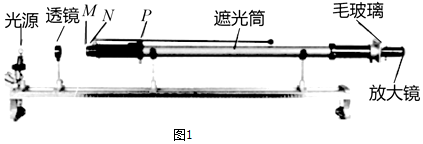
���� ��1��Ϊ��ȡ��ɫ�߹�Դ���ڹ����ϲ�������ͼ������ɫ��Դ����Ҫ���˹�Ƭ�����졢˫�졢�ڹ�Ͳ������
��2�����������Ķ������ڹ̶��̶ȶ������Ͽɶ��̶ȶ��������������ϵ�1���͵�6�����Ƽ�ľ�������������Ƶļ�࣮
��3���α꿨�ߵĶ����������߶��������α�������������������˫��������Ƶļ�ʽ�����ɫ��IJ�����
��� �⣺��1��Ϊ�˻�ȡ��ɫ���߹�Դ����Դ����Ӧ�����˹�Ƭ�����죬�����γɵ�������Թ�Դ����˫���������������ˣ�M��N��P������ѧԪ������Ϊ���˹�Ƭ�����졢˫�죮
��ѡ��A��
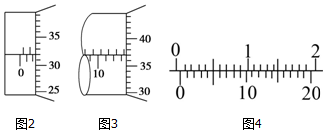
��2�����������Ķ������ڹ̶��������Ͽɶ���������ͼ2�еĶ���Ϊ2mm+0.01��32.0mm=2.320mm��ͼ3�еĶ���Ϊ13.5mm+0.01��37.0mm=13.870mm�������������Ƶļ��$��x=\frac{13.870-2.320}{5}mm$=2.31mm��
��3���α꿨�ߵĶ���Ϊ0+0.05��6mm=0.30mm������$��x=\frac{L}{d}��$�ã���ɫ��IJ�����=$\frac{d•��x}{L}=\frac{0.30��1{0}^{-3}��2.31��1{0}^{-3}}{0.875}$m=792nm��
�ʴ�Ϊ����1��A����2��13.870��2.31����3��0.30��792��
���� ���⿼����ʵ��װ�á����Ƽ�ʽ��Ӧ�ã�֪��˫�����ʵ���ԭ��������Ӧ��˫��������� ��ʽ������ȷ���⣮


 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���˹ΤԤ�Բ���ʵ����֤�˵�Ų��Ĵ��� | |
| B�� | �����ݳ��ֲ�ɫ�������ɹ�ĸ���������ɵ� | |
| C�� | ij�����ٶ�Ϊ0.5c�ķɴ��ϴ�һ��Դ��������������ڵ�����ٶ�ӦΪ1.5c | |
| D�� | ����ͬһ�ϰ������Խ��ĹⲨԽ�����ƹ�ȥ | |
| E�� | ��Դ��۲�����Կ���ʱ���۲��������յ�Ƶ�ʴ�����Դ��Ƶ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
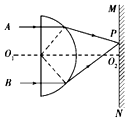 ��ͼ��ʾ��O1O2�ǰ�Բ���β�����ĶԳ����ֽ��Ľ��ߣ�A��B�ǹ���O1O2��Ⱦ���ƽ�е�������ͬ��ɫϸ�������Ӳ������ҷ������Ĺ�·��ͼ��ʾ��MN�Ǵ�ֱ��O1O2���õĹ�������O1O2���������ƶ��������������ϵõ�һ�����P�����ݸù�·ͼ������˵����ȷ���ǣ�������
��ͼ��ʾ��O1O2�ǰ�Բ���β�����ĶԳ����ֽ��Ľ��ߣ�A��B�ǹ���O1O2��Ⱦ���ƽ�е�������ͬ��ɫϸ�������Ӳ������ҷ������Ĺ�·��ͼ��ʾ��MN�Ǵ�ֱ��O1O2���õĹ�������O1O2���������ƶ��������������ϵõ�һ�����P�����ݸù�·ͼ������˵����ȷ���ǣ�������| A�� | �ò������A��������ʱȶ�B���������С | |
| B�� | A��ӿ�������ò��������Ƶ�ʱ�� | |
| C�� | �ڸò������У�A���B��Ĵ����ٶȴ� | |
| D�� | �������A��IJ�����B��IJ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | �� | C�� | ���ļ��ٶ� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ����������У�ͬһʱ�̼��ٶȱ��ҵ��ٶȴ� | |
| B�� | ����������У�ͬһʱ�̼��ٶȱ��ҵ��ٶ�С | |
| C�� | �ס����ڿ������˶���ʱ��֮��Ϊ1��2 | |
| D�� | �����ʱ���Ҿ����ĸ߶�ΪH |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 5cm | B�� | 20cm | C�� | 50cm | D�� | 80cm |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
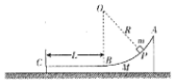 ��ͼ��ʾ��һ��������ˮƽ�����ϣ���AB��Ϊһ�뾶R=1.0m�Ĺ⻬Բ�������BC��Ϊһ����L=0.5m�Ĵֲ�ˮƽ���������������B�㣬�������λ��ͬһ��ֱƽ���ڣ���P�㽫һ������m=0.2kg����飨����Ϊ�ʵ㣩���ٶ��ͷţ���黬��C��ʱǡ�þ�ֹ����֪�����BC�εĶ�Ħ��������=0.1��ȡ�������ٶ�g=10m/s2����
��ͼ��ʾ��һ��������ˮƽ�����ϣ���AB��Ϊһ�뾶R=1.0m�Ĺ⻬Բ�������BC��Ϊһ����L=0.5m�Ĵֲ�ˮƽ���������������B�㣬�������λ��ͬһ��ֱƽ���ڣ���P�㽫һ������m=0.2kg����飨����Ϊ�ʵ㣩���ٶ��ͷţ���黬��C��ʱǡ�þ�ֹ����֪�����BC�εĶ�Ħ��������=0.1��ȡ�������ٶ�g=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
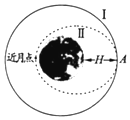 �ҹ����ڽ���12�·��䡰�϶���š����ǣ������ǽ��״�ʵ����������ȡ�������ص�����ͼ��ʾ���衰�϶���š����ھ��������߶�ΪH���Ļ��¹��I������������ΪT������Բ���˶�������ڸù���ϵ�A���ȡ��ʩ���������µ����������߶�Ϊh����Բ������ϣ�����R��ʾ����뾶������������ת����������ǵ�Ӱ�죬��֪��������G���������ж���ȷ���ǣ�������
�ҹ����ڽ���12�·��䡰�϶���š����ǣ������ǽ��״�ʵ����������ȡ�������ص�����ͼ��ʾ���衰�϶���š����ھ��������߶�ΪH���Ļ��¹��I������������ΪT������Բ���˶�������ڸù���ϵ�A���ȡ��ʩ���������µ����������߶�Ϊh����Բ������ϣ�����R��ʾ����뾶������������ת����������ǵ�Ӱ�죬��֪��������G���������ж���ȷ���ǣ�������| A�� | ���϶���š��ڹ��I��A��ļ��ٶȴ����ڹ������A��ļ��ٶ� | |
| B�� | ���϶���š��ڹ��I��A����ٶȵ����ڹ������A����ٶ� | |
| C�� | ���������Ϊ $\frac{4{��}^{2}��R+H��^{3}}{G{T}^{2}}$ | |
| D�� | ���϶���š��ڹ�����ϵ�����Ϊ$\sqrt{\frac{��2R+H+h��^{3}}{8��R+H��^{3}}}$T |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com