
 ��ͼ��ʾ�����費�Ƶ��㹻���⻬ƽ�н���������ˮƽ��н�Ϊ�ȣ�������Ϊl���������ƽ������������������ڴ������н���ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB������ֱ�ڵ���ƽ�����ϣ�������ͬ��������Ϊm��������ͬ�����˼��ҷ����ڵ����ϣ�������ǡ�ô��ڴų����ϱ߽紦���ס������ҲΪl���ھ�ֹ�ͷ��������˵�ͬʱ���Լ�ʩ��һ�ص���ƽ���Ҵ�ֱ�����˵�������ʹ�����ص������µ��˶�������ʼ���Լ��ٶ�a=gsin�����ȼ���ֱ���˶����������ҹн���ų�ʱ���������˶���
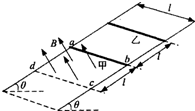
��ͼ��ʾ�����費�Ƶ��㹻���⻬ƽ�н���������ˮƽ��н�Ϊ�ȣ�������Ϊl���������ƽ������������������ڴ������н���ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB������ֱ�ڵ���ƽ�����ϣ�������ͬ��������Ϊm��������ͬ�����˼��ҷ����ڵ����ϣ�������ǡ�ô��ڴų����ϱ߽紦���ס������ҲΪl���ھ�ֹ�ͷ��������˵�ͬʱ���Լ�ʩ��һ�ص���ƽ���Ҵ�ֱ�����˵�������ʹ�����ص������µ��˶�������ʼ���Լ��ٶ�a=gsin�����ȼ���ֱ���˶����������ҹн���ų�ʱ���������˶������� �������ɾ�ֹ���ȼ���ֱ���˶����˶�l����ų�ʱ���������˶�����ƽ��������������������õ��������裬��ţ�ٵڶ����ɣ������������ɽ������ɿ���
�����������������Ľ����ȣ��������غ㶨�ɿ��������Ĺ���
��� �⣺��1��������δ����ų��еĹ����У��ס��ҵļ��ٶ���ͬ�����Ҹս���ų�ʱ����
v2=2ax �� a=gsin��
�� v=$\sqrt{2glsin��}$
�Ҹս���ų�ʱ�������ɸ���ƽ��������$mgsin��=\frac{{B}^{2}{l}^{2}v}{2R}$
$R=\frac{{B}^{2}{l}^{2}\sqrt{2glsin��}}{2mgsin��}$
��2�����ڴų����˶�ʱ����ţ�ٵڶ����ɿ�֪������F��Сʼ�յ��ڰ�������С����$F=\frac{{{B^2}{l^2}v}}{2R}$
v=��gsin�ȣ�t
��� $F=\frac{m{g}^{2}si{n}^{2}��}{\sqrt{2glsin��}}t$
�����ص���ƽ�沢��ֱ�����˼�����
��3�����Ҵ��ͷŵ��ս���ų����������ȼ���ֱ���˶�����Ҫ��ʱ��Ϊt1
l=$\frac{1}{2}��gsin�ȣ�t_1^2$
${t_1}=\sqrt{\frac{2l}{gsin��}}=\frac{l}{gsin��}\sqrt{2glsin��}$
���Ҵӽ���ų����������뿪�ų��Ĺ�����������ֱ���˶�����Ҫ��ʱ��Ϊt2
l=vt2
${t_2}=\frac{l}{{\sqrt{2glsin��}}}=\frac{1}{2gsin��}\sqrt{2glsin��}$
�����뿪�ų�ʱ�����ٶ�v��
v��=��gsin�ȣ���t1+t2��=$\frac{3}{2}\sqrt{2glsin��}$
��״ӿ�ʼ�ͷ������뿪�ų��Ĺ����е�λ��Ϊx
$x=\frac{1}{2}��gsin�ȣ�{��{t_1}+{t_2}��^2}=\frac{9}{4}l$
��������ת�����غ㶨�ɵã�$mgxsin��+mg•2lsin��+{W_F}=2Q+\frac{1}{2}m{v^2}+\frac{1}{2}m{v'^2}$
WF=2Q-mglsin��
�𣺣�1�������˵ĵ���$R=\frac{{B}^{2}{l}^{2}\sqrt{2glsin��}}{2mgsin��}$��
��2���������ڴų������ܵ�����F��ʱ��t�ı仯��ϵʽ$F=\frac{mg2sin2��}{\sqrt{2glsin��}}t$��
��3������F�ڴ˹����������Ĺ�Ϊ2Q-mglsin��
���� ���⿼���˵�Ÿ�Ӧ���ɣ��պϵ�·ŷķ���ɵ��ۺ�Ӧ�ã�Ҫע�������غ��Ӧ�ã���ѧϰ��Ҫע��ѵ�������غ��Ӧ�÷�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
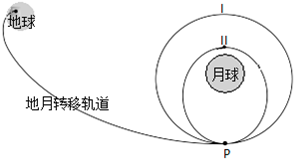 2013��12��2�գ��϶�����̽����˳�����䣮�϶�����Ҫ��һ���Խ�����ص�210���Զ�ص�Լ36.8����ĵ���ת�ƹ����12��10�����Ͼŵ��ʮ�֣���̫�շ����˾���ġ��϶����š��ɴ����ٴγɹ���죬��100km��100km�Ļ���Բ������͵����µ�15km��Զ�µ�100km����Բ�����������ཻ�ڵ�P����ͼ��ʾ������������ʱֻ���������������ã����ڡ��϶����š��ɴ�������˵����ȷ���ǣ�������
2013��12��2�գ��϶�����̽����˳�����䣮�϶�����Ҫ��һ���Խ�����ص�210���Զ�ص�Լ36.8����ĵ���ת�ƹ����12��10�����Ͼŵ��ʮ�֣���̫�շ����˾���ġ��϶����š��ɴ����ٴγɹ���죬��100km��100km�Ļ���Բ������͵����µ�15km��Զ�µ�100km����Բ�����������ཻ�ڵ�P����ͼ��ʾ������������ʱֻ���������������ã����ڡ��϶����š��ɴ�������˵����ȷ���ǣ�������| A�� | �ڹ�������˶�������С���ڹ�������˶������� | |
| B�� | �ع����������P ����ٶȵ����ع����������P ����ٶ� | |
| C�� | �ع����������P ��ļ��ٶȴ����ع����������P ��ļ��ٶ� | |
| D�� | �ڹ�����ϵ������붯��֮�ͱ��ڹ�����ϵ������붯��֮�ʹ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �Შ�ڴ��������У������ϵ��ʵ��˶������ڵIJ������õ�ʱ��Ϊһ������ | |
| B�� | �����IJ���ԶС���ϰ���ijߴ�ʱ�ܹ��������Ե��������� | |
| C�� | ����������������в�Ƶ�ʱ�Ȼ��ͬ | |
| D�� | ����������ЧӦ��ԭ���ǹ۲��ߺͲ�Դ֮�䷢��������˶� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H��${\;}_{2}^{4}$He+${\;}_{0}^{1}$n | |
| B�� | ${\;}_{92}^{235}$+${\;}_{0}^{1}$n��${\;}_{56}^{141}$Ba+${\;}_{36}^{92}$Kr+3${\;}_{0}^{1}$n | |
| C�� | ${\;}_{90}^{234}$Th��${\;}_{91}^{234}$Pa+${\;}_{-1}^{0}$e | |
| D�� | ${\;}_{92}^{238}$U��${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ijͬѧ������ͼ1��ʾ��װ��̽������ƽ���ı��ζ�����ֱ�������а�ֽ��ľ���Ϲ̶�����������С���֣�ϸ��AB��OC�����ڣ��㣬ϸ��AB�ƹ������֣�D��E��ϸ���뻬�ֵ������Ӵ��㣮��ϸ��ĩ��A��B��C�����ֱ���в�ͬ��������ͬ���룬�����ҹ������ֱ���N1��N2��N3��ʾ�������ʵ������Ĺ��룬��ϵͳƽ��ʱ������ؼ�¼���ı����ҹ�����������ظ����ж��ʵ�飮
ijͬѧ������ͼ1��ʾ��װ��̽������ƽ���ı��ζ�����ֱ�������а�ֽ��ľ���Ϲ̶�����������С���֣�ϸ��AB��OC�����ڣ��㣬ϸ��AB�ƹ������֣�D��E��ϸ���뻬�ֵ������Ӵ��㣮��ϸ��ĩ��A��B��C�����ֱ���в�ͬ��������ͬ���룬�����ҹ������ֱ���N1��N2��N3��ʾ�������ʵ������Ĺ��룬��ϵͳƽ��ʱ������ؼ�¼���ı����ҹ�����������ظ����ж��ʵ�飮�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
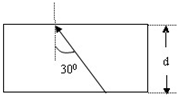 ���ߴ�������n=$\sqrt{2}$������Ϊd�IJ�����������У��������Ϊ30��ʱ�������Ϊ���٣������ڲ���ש�Ĵ����ٶ��Լ�����ʱ����Ƕ��٣�����֪��������д����ٶ�Ϊc��
���ߴ�������n=$\sqrt{2}$������Ϊd�IJ�����������У��������Ϊ30��ʱ�������Ϊ���٣������ڲ���ש�Ĵ����ٶ��Լ�����ʱ����Ƕ��٣�����֪��������д����ٶ�Ϊc���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com