
 如图所示,空间存在一个半径为R0的圆形匀强磁场区域,磁场的方向垂直于纸面向里,磁感应强度的大小为B.有一个粒子源在纸面内沿各个方向以一定速率发射大量粒子,粒子的质量为m、电荷量为+q.将粒子源置于圆心,则所有粒子刚好都不离开磁场.(不考虑粒子的重力及粒子之间的相互作用)
如图所示,空间存在一个半径为R0的圆形匀强磁场区域,磁场的方向垂直于纸面向里,磁感应强度的大小为B.有一个粒子源在纸面内沿各个方向以一定速率发射大量粒子,粒子的质量为m、电荷量为+q.将粒子源置于圆心,则所有粒子刚好都不离开磁场.(不考虑粒子的重力及粒子之间的相互作用)分析 (1)根据几何关系,结合洛伦兹力提供向心力,由牛顿第二定律,即可求解;
(2)由几何关系,可求出运动轨迹的圆心角,根据周期公式,即可求解;
(3)根据矢量法则,可确定磁场方向与大小,再由几何关系,结合周期公式,即可求解.
解答 解:(1)粒子离开出发点最远的距离为轨道半径的2倍,
R0=2r,
根据qvB=$m\frac{{v}^{2}}{r}$,
解得v=$\frac{qB{R}_{0}}{2m}$.
(2)磁场的大小变为$\frac{B}{4}$后,粒子的轨道半径为r1;
${r}_{1}=\frac{mv}{q{B}_{1}}=\frac{4mv}{qB}$=2R0.
根据几何关系可以得到,当弦最长时,运动的时间最长,弦为2R0时最长,圆心角60°
t=$\frac{60°}{360°}T=\frac{4πm}{3qB}$.
(3)根据矢量合成法则,叠加区域的磁场大小为$\frac{B}{2}$,方向向里,
R0以为的区域磁场大小为$\frac{B}{2}$,方向向外.粒子运动的半径为R0,
根据对称性画出情境图,由几何关系可得R1的最小值为$(\sqrt{3}+1){R}_{0}$,
根据周期公式,则有T=$\frac{(\frac{π}{3}+\frac{5}{6}π)•4m}{\frac{qB}{2}}=\frac{28πm}{3qB}$.
答:(1)带电粒子的速率为$\frac{qB{R}_{0}}{2m}$.
(2)粒子在磁场中最长的运动时间为$\frac{4πm}{3qB}$;
(3)R1的最小值为$(\sqrt{3}+1){R}_{0}$,粒子运动的周期为$\frac{28πm}{3qB}$.
点评 洛伦兹力提供圆周运动向心力,根据轨迹关系求出粒子进入磁场中的速度方向,再根据速度关系求出质子在电场中做何种运动,然后根据运动性质求解.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,水平传送带以a1=0.5m/s2的加速度水平向右运动,传送带两端距离是s=14m,将一质量为m的物体轻放在传送带左端A,此时传送带的顺时速度为v0=1m/s,已知传送带与物体间的动摩擦因数为μ=0.1,求物体从传送带一段运动到另一端所需时间.
如图所示,水平传送带以a1=0.5m/s2的加速度水平向右运动,传送带两端距离是s=14m,将一质量为m的物体轻放在传送带左端A,此时传送带的顺时速度为v0=1m/s,已知传送带与物体间的动摩擦因数为μ=0.1,求物体从传送带一段运动到另一端所需时间.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,两根足够长的光滑金属平行导轨,导轨平面与水平面的夹角为30°,上端连接电阻R=4Ω,空间有垂直于导轨平面的匀强磁场,磁感应强度B=1T.一根与导轨接触良好的质量m=0.2Kg,长度L=1m,电阻r=1Ω的金属棒MN有静止开始沿导轨下滑.求:(金属导轨的电阻忽略不计,g取10m/s2)
如图所示,两根足够长的光滑金属平行导轨,导轨平面与水平面的夹角为30°,上端连接电阻R=4Ω,空间有垂直于导轨平面的匀强磁场,磁感应强度B=1T.一根与导轨接触良好的质量m=0.2Kg,长度L=1m,电阻r=1Ω的金属棒MN有静止开始沿导轨下滑.求:(金属导轨的电阻忽略不计,g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题

| v2/(m2•a-2) | 0.160 | 0.241 | 0.320 | 0.401 | 0.409 |
| h/m | 10.0 | 15.0 | 20.0 | 25.0 | 30.0 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
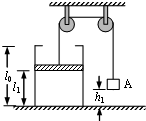 高l0=15cm的圆柱形气缸开口向上放置在水平面上,开口处两侧有挡板,如图所示.缸内有一可自由移动的活塞封闭了一定质量的理想气体,不可伸长的细线一端系在活塞上,另一端跨过两个定滑轮连着物体A.开始时,气体温度T1=300K,活塞到缸底的距离l1=10cm,物体A的底部离地h1=4cm,对气缸内的气体缓慢加热使活塞缓慢上升.试求:物体A刚触地时,缸内气体的温度.
高l0=15cm的圆柱形气缸开口向上放置在水平面上,开口处两侧有挡板,如图所示.缸内有一可自由移动的活塞封闭了一定质量的理想气体,不可伸长的细线一端系在活塞上,另一端跨过两个定滑轮连着物体A.开始时,气体温度T1=300K,活塞到缸底的距离l1=10cm,物体A的底部离地h1=4cm,对气缸内的气体缓慢加热使活塞缓慢上升.试求:物体A刚触地时,缸内气体的温度.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图为“探究电磁感应现象”的实验装置.
如图为“探究电磁感应现象”的实验装置.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 甲、乙两质点从同一地点出发沿同一直线运动,它们的速度(v-t)图象分别由图中直线I和Ⅱ表示,则两质点( )
甲、乙两质点从同一地点出发沿同一直线运动,它们的速度(v-t)图象分别由图中直线I和Ⅱ表示,则两质点( )| A. | 甲、乙两物体在2s内的平均速度相等 | |
| B. | 甲、乙两物体做相向运动 | |
| C. | 4s末甲、乙的速度相等 | |
| D. | 第2s末甲、乙的速度相等 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com