
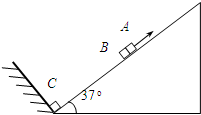
 如图所示,可视为质点的物块A、B、C放在倾角为37°、长L=2m的固定斜面上,物块与斜面间的动摩擦因数μ=0.5.A与B紧靠在一起,C紧靠在固定挡板上.物块的质量分别为mA=0.8kg、mB=0.4kg.其中A不带电,B、C的带电量分别为qB=+4×10-5C、
如图所示,可视为质点的物块A、B、C放在倾角为37°、长L=2m的固定斜面上,物块与斜面间的动摩擦因数μ=0.5.A与B紧靠在一起,C紧靠在固定挡板上.物块的质量分别为mA=0.8kg、mB=0.4kg.其中A不带电,B、C的带电量分别为qB=+4×10-5C、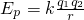 ).求:
).求: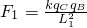
 ①
①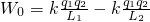


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中物理 来源: 题型:
 (2013?普陀区一模)如图所示,可视为质点的物块A、B、C放在倾角为37°、长L=2m的固定斜面上,物块与斜面间的动摩擦因数μ=0.5.A与B紧靠在一起,C紧靠在固定挡板上.物块的质量分别为mA=0.8kg、mB=0.4kg.其中A不带电,B、C的带电量分别为qB=+4×10-5C、
(2013?普陀区一模)如图所示,可视为质点的物块A、B、C放在倾角为37°、长L=2m的固定斜面上,物块与斜面间的动摩擦因数μ=0.5.A与B紧靠在一起,C紧靠在固定挡板上.物块的质量分别为mA=0.8kg、mB=0.4kg.其中A不带电,B、C的带电量分别为qB=+4×10-5C、| q1q2 | r |
查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,可视为质点的小球用细线拉住并放在光滑斜面上,斜面体放在光滑水平面上,水平力F作用在斜面体上使之处于静止.细线的拉力为T,斜面对小球的支持力大小为FN.缓慢向左推动斜面体在小球未脱离斜面的过程中,下列说法中正确的是( )
如图所示,可视为质点的小球用细线拉住并放在光滑斜面上,斜面体放在光滑水平面上,水平力F作用在斜面体上使之处于静止.细线的拉力为T,斜面对小球的支持力大小为FN.缓慢向左推动斜面体在小球未脱离斜面的过程中,下列说法中正确的是( )查看答案和解析>>
科目:高中物理 来源: 题型:
 (1)一单色光照到某金属表面时,有光电子从金属表面逸出,下列说法中正确的是:下列描述中正确的是
(1)一单色光照到某金属表面时,有光电子从金属表面逸出,下列说法中正确的是:下列描述中正确的是查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com