4．如图所示，在光滑的水平地面上有一个表面光滑的物块P，它的质量为M，一长为L的轻杆下端用光滑铰链连接于O点，O点固定于地面上，轻杆的上端连接着一个可视为质点的小球Q，它的质量为m，且M=5m．开始时，小球斜靠在物块左侧，它距地面的高度为h，物块右侧受到水平向左推力F的作用，整个装置处于静止状态．若现在撤去水平推力F，则下列说法中正确的是（　　）

	A．	物块先做匀加速运动，后做匀速运动
	B．	在小球和物块分离前，当轻杆与水平面的夹角为θ时，小球的速度大小$\sqrt{\frac{2g（h-Lsinθ）}{{1+5si{n^2}θ}}}$
	C．	小球与物块分离时，小球一定只受重力作用
	D．	在小球落地之前，小球的机械能一直减少

3．一宇宙人在太空（那里重力可以忽略不计）玩垒球．辽阔的太空球场半侧为均匀电场，场强为E，另半侧为均匀磁场，磁感应强度为B，电场和磁场的分界面为平面，电场方向与界面垂直，磁场方向垂直纸面向里．宇宙人位于电场一侧的P点，O点是P点至界面垂线的垂足，如图所示，现有三个质量相等的垒球，其中垒球1号与垒球2号带电量相同（带负电），垒球3号不带电．且宇宙人每次都是从同一点P投出垒球．宇宙人先在P点由静止释放垒球1号，间隔时间T后以一定初速度v₁水平向左抛出垒球2号，垒球2号第一次到达界面时刚好与第二次到达界面的垒球1号相碰．
（1）试求垒球2号抛出时初速度v₁的大小．
（2）试求垒球1号的比荷大小．
（3）假设宇宙人在将垒球1号由静止释放的同时，将垒球3号以大小为v₂的初速度水平向左抛出，结果垒球1号刚好可以与垒球3号相碰，假设PO=$\frac{πE}{2B}$T，试求v₂的大小．（该题不考虑垒球之间的相互作用力）

2．如图甲所示，竖直面MN的左侧空间中存在竖直向上的匀强电场（上、下及左侧无边界）．一个质量为m、电荷量为q，可视为质点的带正电小球，以水平初速度v₀沿PQ向右做直线运动．若小球刚经过D点时（t=0），在电场所在空间叠加如图乙所示随时间周期性变化、垂直纸面向里的匀强磁场，使得小球再次通过D点时与PQ连线成60°角．已知D、Q间的距离为（$\sqrt{3}$+1）L，t₀小于小球在磁场中做圆周运动的周期，忽略磁场变化造成的影响，重力加速度为g．求：

（1）电场强度E的大小；
（2）t₀与t₁的比值；
（3）小球过D点后将做周期性运动．则当小球运动的周期最大时，求出此时的磁感应强度B₀及运动的最大周期T_m的大小，并在图中画出此情形下小球运动一个周期的轨迹．

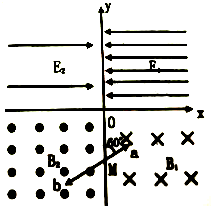1．在xOy平面第Ⅰ象限中，存在沿x轴负方向的匀强电场，场强为E₁=$\frac{3πBl}{2{t}_{0}}$，第Ⅱ象限中存在沿x轴正方向的匀强电场，场强为E₂=$\frac{πBl}{2{t}_{0}}$，在第Ⅲ、Ⅳ象限中，存在垂直于xOy平面方向的匀强磁场，方向如图所示．磁感应强度B₁=B，B₂=2B．带电粒子a、b同时从y轴上的点M（0，-$\sqrt{3}$l）以不同的速率向相反方向射出，射出时粒子a的速度方向与y轴正方向成60°角，经过时间t₀，粒子a、b同时第一次垂直x轴进入电场，不计粒子重力和两粒子间相互作用．求：
（1）粒子a的比荷及射出磁场时的位置；
（2）粒子a、b射出磁场时速度的大小；
（3）进入电场后，粒子a、b先后第一次到达y轴上的P、Q两点（图中未画出），求P、Q两点间的距离．

5．下列说法正确的（　　）

	A．	${\;}_{90}^{234}$Th→${\;}_{91}^{234}$Pa+X 中的X是电子
	B．	${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{8}^{17}$O+${\;}_{1}^{1}$H是α衰变
	C．	${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n是核聚变
	D．	${\;}_{34}^{82}$Se→${\;}_{36}^{82}$Kr+2${\;}_{-1}^{0}$e是核裂变

4．在用油膜法粗测分子直径的实验中，在哪些方面作了理想化的假设将油膜看成单分子膜，将油酸分子看做球形，认为油酸分子是一个紧挨一个的；实验中滴在水面的是油酸酒精溶液而不是纯油酸，且只能滴一滴，这是因为纯油酸粘滞力较大，直接测量体积时误差太大；在将油酸酒精溶液滴向水面前，要先在水面上均匀撒些痱子粉，这样做是为了界定油膜大小的边界．

3．利用霍尔效应制作的霍尔元件以及传感器，广泛应用于测量和自动控制等领域．如图1，将一金属或半导体薄片垂直置于磁场B中，在薄片的两个侧面a、b间通以电流I时，另外两侧c、f间产生电势差，这一现象称为霍尔效应．其原因是薄片中的移动电荷受洛伦兹力的作用向一侧偏转和积累，于是c、f间建立起电场E_H，同时产生霍尔电势差U_H．当电荷所受的电场力与洛伦兹力处处相等时，E_H和U_H达到稳定值，U_H的大小与I和B以及霍尔元件厚度d之间满足关系式U_H=R_H$\frac{IB}{d}$，其中比例系数R_H称为霍尔系数，仅与材料性质有关．

（1）设半导体薄片的宽度（c、f间距）为l，写出U_H和E_H的关系式；若半导体材料是电子导电的，判断图1中c、f哪端的电势高；
（2）已知半导体薄片内单位体积中导电的电子数为n，电子的电荷量为e，导出霍尔系数R_H的表达式．（通过横截面积S的电流I=nevS，其中v是导电电子定向移动的平均速率）；
（3）图2是霍尔测速仪的示意图，将非磁性圆盘固定在转轴上，圆盘的周边等距离地嵌装着m个永磁体，相邻永磁体的极性相反．霍尔元件置于被测圆盘的边缘附近．当圆盘匀速转动时，霍尔元件输出的电压脉冲信号图象如图3所示．若在时间t内，霍尔元件输出的脉冲数目为P，导出圆盘转速N的表达式．

2．图1中所示装置可以用来测量硬弹簧（即劲度系数较大的弹簧）的劲度系数k．电源的电动势为E，内阻可忽略不计；滑动变阻器全长为l，重力加速度为g，V为理想电压表．当木板上没有放重物时，动变阻器的触头位于图1中a点，此时电压表示数为零．在木板上放置质量为m的重物，滑动变阻器的触头随木板一起下移．由电压表的示数U及其它给定条件，可计算出弹簧的劲度系数k．

（1）写出m、U与k之间所满足的关系式．$m=\frac{lk}{Eg}U$
（2）己知E=1.50V，l=12.0cm，g=9.80m/s²．测量结果如表：

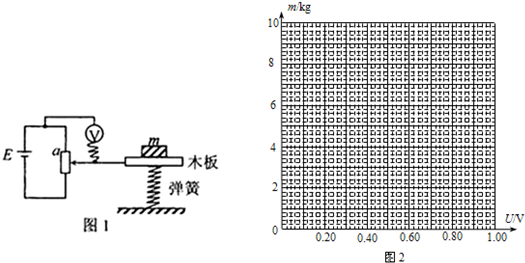
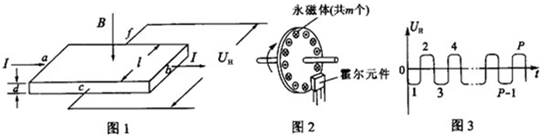
m（kg）	1.00	1.50	3.00	4.50	6.00	7.50
U（V）	0.108	0.154	0.290	0.446	0.608	0.740

①在图2中给出的坐标纸上利用表中数据描出m-U直线．
②m-U直线的斜率为10.0kg/V．
③弹簧的劲度系数k=1.24×10³N/m．（保留3位有效数字）

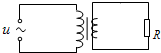1．如图所示，理想变压器原、副线圈的匝数比为2：1，电阻R=55.0Ω，原线圈两端接一正弦式交变电流，电压u随时间t变化的规律为u=110$\sqrt{2}$sin20πt（V），时间t的单位是s．那么，通过电阻R的电流有效值和频率分别为（　　）

A．

1.0A、20Hz

B．

$\sqrt{2}$A、20Hz

C．

$\sqrt{2}$A、10Hz

D．

1.0A、10Hz

20．如图所示为一理想变压器，S为一单刀双掷开关，P为滑动变阻器的滑动片，U₁为加在原线圈两端的电压，I₁为原线圈中的电流．那么（　　）

	A．	保持U1及P的位置不变，S由1拨到2时，I1将增大
	B．	保持U1及P的位置不变，S由2拨到1时，R消耗的功率减小
	C．	保持U1不变，S拨到1，当P下滑时，I1将增大
	D．	保持P的位置不变时，S拨到1，当U1增大时，I1将增大