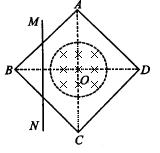
如图所示，边长为L＝2m的正方形导线框ABCD和一金属棒MN由粗细相同的同种材料制成，每米长电阻为R₀＝1/m，以导线框两条对角线交点O为圆心，半径r＝0.5m的匀强磁场区域的磁感应强度为B＝0.5T，方向垂直纸面向里且垂直于导线框所在平面，金属棒MN与导线框接触良好且与对角线AC平行放置于导线框上。若棒以v＝4m/s的速度沿垂直于AC方向向右匀速运动，当运动至AC位置时，求（计算结果保留二位有效数字）：

（1）棒MN上通过的电流强度大小和方向；

（2）棒MN所受安培力的大小和方向。

一质点在一平面内运动，其轨迹如图所示。它从A点出发，以恒定速率经时间t到B点，图中x轴上方的轨迹都是半径为R的半圆，下方的都是半径为r的半圆。

（1）求此质点由A到B沿x轴运动的平均速度。

（2）如果此质点带正电，且以上运动是在一恒定（不随时间而变）的磁场中发生的，试尽可能详细地论述此磁场的分布情况。不考虑重力的影响。

氢原子基态能量E₁=－13.6eV，电子绕核做圆周运动的半径r₁=0.53×10^－10m. 求氢原子处于n=4激发态时：（1）原子系统具有的能量？（2）电子在n=4轨道上运动的动能？（已知能量关系，半径关系×10⁹Nm²/c²）

太阳的能量来自下面的反应：四个质子（氢核）聚变成一个粒子，同时发射两个正电子和两个没有静止质量的微子，若太阳辐射能量的总功率为P，质子H、氦核He、正电子e的质量分别为m_p、m_a、m_e，真空中的光速为c，求：

   （1）写出核的应方程式。

   （2）核反应所释放的能量△E。

   （3）在t时间内参与上述热核反应的质子数目。

某植物园的建筑屋顶有太阳能发电系统，用来满足园内用电需要。已知该发电系统的输出功率为1.0×10⁵W，输出电压为220V。求：

①按平均每天太阳照射6小时计，该发电系统一年（365天计）能输出多少电能？

②该太阳能发电系统除了向10台1000W的动力系统正常供电外，还可以同时供园内多少盏功率为100W，额定电压为220V的照明灯正常工作？

③由于发电系统故障，输出电压降为110V，此时每盏功率为100W、额定电压为220V的照明灯消耗的功率等是其正常工作时的多少倍？

三个闭合矩形线框Ⅰ、Ⅱ、Ⅲ处在同一竖直平面内，在线框的正上方有一条固定的长直导线，导线中通有自左向右的恒定电流，如图所示，若三个闭合线框分别做如下运动：Ⅰ沿垂直长直导线向下运动，Ⅱ沿平行长直导线方向平动，Ⅲ绕其竖直中心轴OO′转动.

 (1)在这三个线框运动的过程中，哪些线框中有感应电流产生?方向如何?

 (2)线框Ⅲ转到图示位置的瞬间，是否有感应电流产生?

如图所示，4米长的传送带与水平成37°角。开始时传送带静止，一质量为m=5kg的滑块以=8m/s的初速度从传送带底端沿传送带上滑。已知滑块与传送带之间的动摩擦因数=0.5，当滑块滑至传送带正中间时，突然开动传送带，使之以m/s的速度沿逆时针方向运动。（g取10m/s²，sin37°=，cos37°=）求：

（1）滑块沿传送带能够上滑的最大距离；

（2）从滑块滑上传送带到离开的整个过程中，传送带对滑块所做的功。

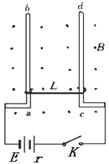
如图所示，ab、cd是两根固定的竖直光滑的足够长金属导轨，导轨上套有一根可滑动的金属细棒，整个装置放在磁感应强度B=0.5T的水平匀强磁场中。已知棒长L=10cm，电阻R=0.2Ω，质量m=20g，开始时处于静止状态。电池电动势E=1.5V，内阻r=0.1Ω，导轨的电阻、空气阻力均不计，取g=10m/s²。当电键K闭合后，试求：

（1）棒L的最大加速度；

（2）棒L的最大速度；

（3）棒L达到最大速度后，棒L发热消耗的功率与整个电路消耗的功率之比；

（4）若棒L从静止到速度达到最大过程中上升了s=10m，则在这过程中，安培力对棒L所做的功是多少？

如图所示，位于介质Ⅰ和Ⅱ分界面上的波源S，产生两列分别沿x轴负方向与正方向传播的机械波。若在两种介质中波的频率及传播速度分别为f₁、f₂和v₁、v₂，则

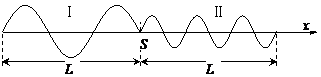A、f₁＝2f₂  v₁＝v₂

B、f₁＝f₂  v₁＝2v₂

C、f₁＝f₂  v₁＝0.5v₂

D、f₁＝0.5f₂  v₁＝v₂

如图所示，在光滑水平地面上，有一质量m₁＝ 4.0kg的平板小车，小车的右端有一固定的竖直挡板，挡板上固定一轻质细弹簧。位于小车上A点处质量m₂＝1.0kg的木块(可视为质点)与弹簧的左端相接触但不连接，此时弹簧与木块间无相互作用力。木块与A点左侧的车面之间的动摩擦因数μ＝ 0.40，木块与A点右侧的车面之间的摩擦可忽略不计。现小车与木块一起以v₀＝ 2.0m/s的初速度向右运动，小车将与其右侧的竖直墙壁发生碰撞，已知碰撞时间极短，碰撞后小车以v ₁＝ 1.0m/s的速度反向弹回，已知重力加速度g取10m/s²，弹簧始终处于弹性限度内。求:

（1）小车撞墙后弹簧的最大弹性势能；

（2）要使木块最终不从小车上滑落，则车面A点左侧粗糙部分的长度应满足什么条件?