
网址:http://1010pic.com/paper/timu/5152313.html[举报]
9. 函数与方程:
(1)理解函数的零点和方程的根的关系、根的存在性定理,了解单调函数零点唯一性的判定。
(2)结合函数的图像,能够用二分法求相应方程的近似解,并注重这种思想方法的应用.
III.导数及其应用
[考纲要求]
(1)导数概念及其几何意义
① 了解导数概念的实际背景.
② 理解导数的几何意义.
(2)导数的运算
① 能根据导数定义,求函数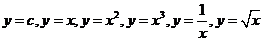 的导数.
的导数.
② 能利用表1给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数,能求简单的复合函数(仅限于形如f(ax+b))的导数.
表1:常见基本初等函数的导数公式和常用导数运算公式:
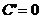 (C为常数);
(C为常数);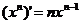 , n∈N+;
, n∈N+;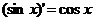 ;
;
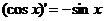 ;
;  ;
;  ;
; 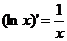 ;
;  .
.
法则1 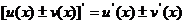 .
.
法则2
 .
.
法则3 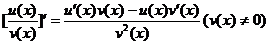 .
.
(3)导数在研究函数中的应用
① 了解函数单调性和导数的关系;能利用导数研究函数的单调性,会求函数的单调区间(对多项式函数一般不超过三次).
②了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、极小值(对多项式函数一般不超过三次);会求闭区间上函数的最大值、最小值(对多项式函数一般不超过三次).
(4)生活中的优化问题:会利用导数解决某些实际问题.
(5)定积分与微积分基本定理
① 了解定积分的实际背景,了解定积分的基本思想,了解定积分的概念.
② 了解微积分基本定理的含义.
[07年考纲与06年考纲的比较]
|
07考纲(新) |
06考纲(旧) |
|
理解导数的几何意义. |
掌握函数在一点处的导数的定义和导数的几何意义 |
|
能求简单的复合函数(仅限于形如f(ax+b))的导数. |
了解复合函数的求导法则,会求某些简单函数的导数. |
|
了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、极小值,对多项式函数一般不超过三次;会求闭区间上函数的最大值、最小值,对多项式函数一般不超过三次. |
了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号);会求一些实际问题(一般指单峰函数)的最大值和最小值. |
|
定积分与微积分基本定理,推理与证明 |
|
[目标定位]
(1)了解导数概念的某些实际背景(如瞬时速度、加速度、光滑曲线切线的斜率等),掌握函数在一点处的导数的定义和导数的几何意义,理解导函数的概念.
(2)熟记基本求导公式(C,xm(m为有理数),sinx,cosx,ex,ax,lnx,logax的导数),掌握两个函数和、差、积、商的求导法则.了解复合函数的求导法则,会求某些简单函数的导数.
(3)了解可导函数的单调性与其导数的关系,了解可导函数在某点取得极值的必要条件和充分条件(导数在极值点两侧异号),会求一些实际问题(一般指单峰函数)的最大值和最小值.
[新增内容]:定积分与微积分基本定理
微积分基本定理是高等数学的基础,在高中数学中要求较低,目标层次为了解,只要求学生能根据微积分基本定理求一些较为简单的定积分,能利用定积分的几何意义求面积.
[课时建议] 8课时.
[重点与难点]
(1) 利用求导公式、运算法则求导函数。
(2) 重视利用导数定义和几何意义解题,导函数的几何意义是过曲线上点作曲线切线的斜率,导函数的代数意义是其符号可以判断函数的单调性。
(3) 理解利用导数研究函数的单调性和极值.
(4) 导数的应用
(5) 会求简单函数的定积分.
[07年新课程地区高考试卷统计分析]
|
知识点 |
题型 |
广东 |
山东 |
宁夏海南 |
|
|
含有全称命题的否定 |
选择 |
|
√ |
√ |
|
|
对数函数的定义域、集合运算 |
选择 |
√ |
|
|
|
|
指数不等式、集合运算 |
选择 |
|
√ |
|
|
|
函数的图象 |
选择 |
√ |
|
|
|
|
幂函数、函数奇偶性 |
选择 |
|
√ |
|
|
|
充要条件 |
选择 |
|
√ |
|
|
|
过曲线上点的切线所围成的面积 |
选择 |
|
|
√ |
|
|
已知函数奇偶性求参数 |
填空 |
|
|
√ |
|
|
对数函数图象的定点、基本不等式 |
填空 |
|
√ |
|
|
|
二次函数的零点 |
解答 |
√ |
|
|
|
|
以自然对数为背景的极值等问题 |
解答 |
|
√ |
√ |
|
|
以二次函数、二次方程的根、导数为背景的数列问题 |
解答 |
√ |
|
|
|
|
集合、运算信息题 |
选择 |
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考答案
1.C 2. C 3.C
4.D 5.C 6.B 7.C
8.A 9. 6 10. 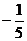
11. 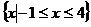 ;
;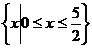 12. 4 13.
12. 4 13. 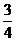 14. ①④⑤
14. ①④⑤
15. 解:由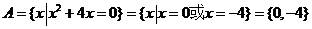 .
.
∵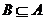 ,∴
,∴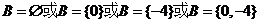 .
.
当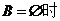 ,即
,即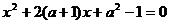 无实根,由
无实根,由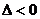 ,
,
即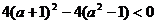 ,解得
,解得 ;
;
当 时,由根与系数的关系:
时,由根与系数的关系: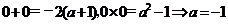 ;
;
当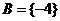 时,由根与系数的关系:
时,由根与系数的关系: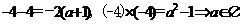 ;
;
当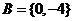 时,由根与系数的关系:
时,由根与系数的关系: ;
;
综上所得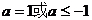 .
.
16. 解法一: (Ⅰ)由图象可知,在(-∞,1)上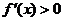 ,在(1,2)上
,在(1,2)上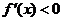 ,在
,在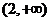 上
上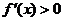 , 故
, 故 在
在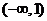 ,
,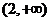 上递增,在(1,2)上递减,因此
上递增,在(1,2)上递减,因此 在
在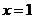 处取得极大值,所以
处取得极大值,所以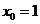 .
.
(Ⅱ)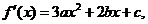 由
由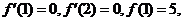 得
得 解得
解得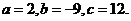
解法二:(Ⅰ)同解法一.
(Ⅱ)设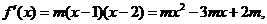
又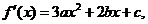 所以
所以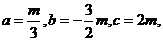
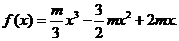
由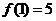 ,即
,即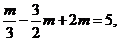 得
得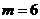 ,
所以
,
所以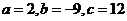 .
.
17. 解:(1) 当 时,
时, ,
,
则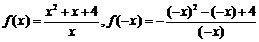
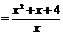
∴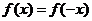 当
当 时,
时,  ,
,
则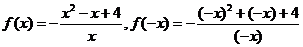
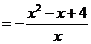 ,
,
∴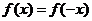
综上所述, 对于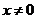 , 都有
, 都有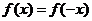 ,∴ 函数
,∴ 函数 是偶函数。
是偶函数。
(2)当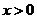 时,
时, 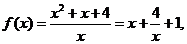
设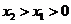 , 则
, 则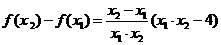 .
.
当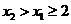 时,
时, 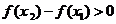 ;
;
当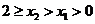 时,
时, 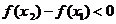 ,
,
∴ 函数 在
在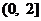 上是减函数, 函数
上是减函数, 函数 在
在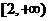 上是增函数。
上是增函数。
(3)由(2)知, 当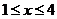 时,
时, 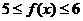 ,
,
又由(1)知, 函数 是偶函数, ∴ 当
是偶函数, ∴ 当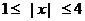 时,
时, 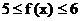 ,
,
∴若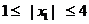 ,
,  , 则
, 则 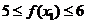 ,
, 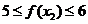 ,
,
∴ , 即
, 即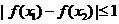 .
.
18.解:(1)因为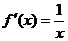 ,所以
,所以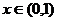 时,
时,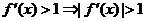 ,
,
即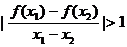 . 当
. 当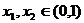 时,
时, ;
;
(2)由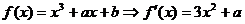 ,
,
当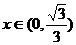 时,
时,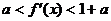 ,因为
,因为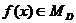 ,
,
所以 ,即
,即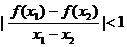 ;
;
所以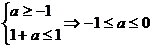 即为所求.
即为所求.
评析:本题应用常规解法,解答较为繁琐;若用导数的几何意义,则十分简单。
19. 解:(1)设方案甲与方案乙的用水量分别为x与z,由题设有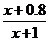 =0.99,解得x=19.
=0.99,解得x=19.
由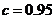 得方案乙初次用水量为3, 第二次用水量y满足方程:
得方案乙初次用水量为3, 第二次用水量y满足方程:
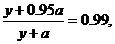 解得y=4
解得y=4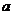 ,故z=4
,故z=4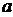 +3.即两种方案的用水量分别为19与4
+3.即两种方案的用水量分别为19与4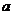 +3.
+3.
因为当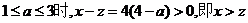 ,故方案乙的用水量较少.
,故方案乙的用水量较少.
(2)设初次与第二次清洗的用水量分别为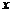 与
与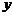 ,类似(I)得
,类似(I)得
 ,
,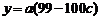 (*)
(*)
于是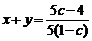 +
+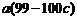

当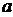 为定值时,
为定值时,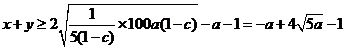 ,
,
当且仅当 时等号成立.此时
时等号成立.此时
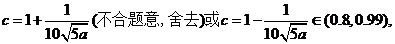
将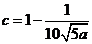 代入(*)式得
代入(*)式得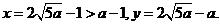
故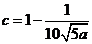 时总用水量最少, 此时第一次与第二次用水量分别为
时总用水量最少, 此时第一次与第二次用水量分别为
 , 最少总用水量是
, 最少总用水量是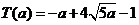 .
.
当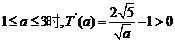 ,故T(
,故T(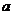 )是增函数(也可以用二次函数的单
)是增函数(也可以用二次函数的单
调性判断).这说明,随着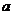 的值的最少总用水量, 最少总用水量最少总用水量.
的值的最少总用水量, 最少总用水量最少总用水量.
20. 解:(Ⅰ)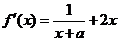 ,依题意有
,依题意有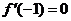 ,故
,故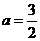 .
.
从而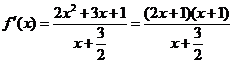 .
.
 的定义域为
的定义域为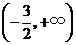 ,当
,当 时,
时,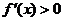 ;
;
当 时,
时,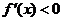 ;当
;当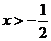 时,
时,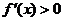 .
.
从而, 分别在区间
分别在区间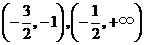 单调增加,在区间
单调增加,在区间 单调减少.
单调减少.
(Ⅱ) 的定义域为
的定义域为 ,
,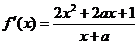 .
.
方程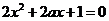 的判别式
的判别式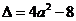 .
.
(ⅰ)若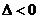 ,即
,即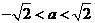 ,在
,在 的定义域内
的定义域内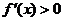 ,故
,故 的极值.
的极值.
(ⅱ)若 ,则
,则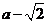 或
或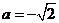 .
.
若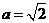 ,
,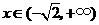 ,
,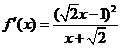 .
.
当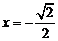 时,
时,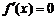 ,当
,当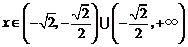 时,
时,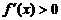 ,所以
,所以 无极值.
无极值.
若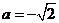 ,
,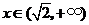 ,
,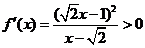 ,
, 也无极值.
也无极值.
(ⅲ)若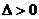 ,即
,即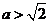 或
或 ,则
,则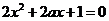 有两个不同的实根
有两个不同的实根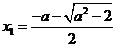 ,
,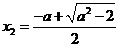 .
.
当 时,
时,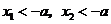 ,从而
,从而 有
有 的定义域内没有零点,故
的定义域内没有零点,故 无极值.
无极值.
当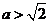 时,
时,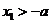 ,
,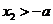 ,
, 在
在 的定义域内有两个不同的零点,由根值判别方法知
的定义域内有两个不同的零点,由根值判别方法知 在
在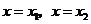 取得极值.
取得极值.
综上, 存在极值时,
存在极值时,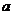 的取值范围为
的取值范围为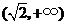 .
.
 的极值之和为
的极值之和为
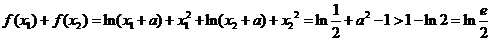 .
.