
高2009级一诊模拟(理科)数学试题
一.选择题:(每小题5分,共60分)
1.设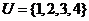 ,且
,且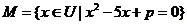 ,若
,若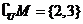 ,则实数
,则实数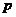 的值为
的值为
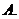
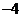
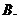
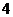
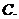
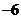
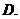
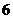
2.等差数列{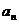 }中,若
}中,若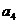 +
+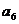 +
+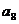 +
+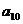 +
+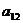 =120,则
=120,则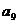 -
-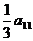 的值是
的值是
A.14 B.
3.已知向量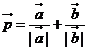 ,其中
,其中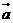 、
、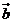 均为非零向量,则
均为非零向量,则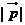 的取值范围是
的取值范围是
A.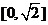 B。
B。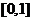 C。
C。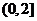 D。
D。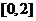
4.编号为1、2、3、4、5的五个人分别去坐编号为1、2、3、4、5的五个座位,其中有且只有两个的编号与座位号一致的坐法是
A 10种 B 20种 C 30种 D 60种
5.若(1+mx)6=a0+a1x+a2x2+…+a6x6且a1+a2+…+a6=63,则实数m的值为.
A.
1
B.
6.已知数列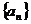 是由正数组成的数列,
是由正数组成的数列,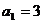 ,且满足
,且满足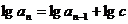 ,其中
,其中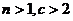 ,则
,则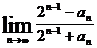 等于
等于
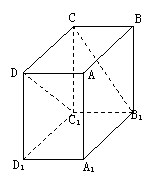 A. -1
B.
A. -1
B. 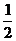 D.
D. 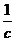
7.一个篮球运动员投篮一次得3分的概率为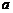 ,得2分的概率为
,得2分的概率为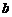 ,不得分的概率为
,不得分的概率为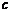 (
(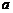 、
、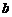 、
、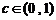 ),已知他投篮一次得分的数学期望为2(不计其它得分情况),则
),已知他投篮一次得分的数学期望为2(不计其它得分情况),则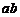 的最大值为
的最大值为
A.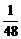 B.
B.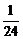 C.
C.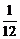 D.
D.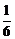
8.在长方体ABCD-A1B
A.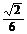 B.
B. 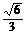 C.
C. 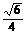 D.
D. 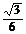
9.设函数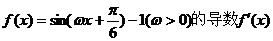 的最大值为3,则f(x)的图象的一条对称轴的方程是
的最大值为3,则f(x)的图象的一条对称轴的方程是
A.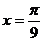 B.
B.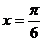 C.
C.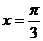 D.
D.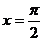
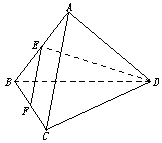 10.如图在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且AC=1,则正三棱锥A-BCD的外接球的体积是
10.如图在正三棱锥A-BCD中,E、F分别是AB、BC的中点,EF⊥DE,且AC=1,则正三棱锥A-BCD的外接球的体积是

11.已知函数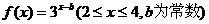 的图象经过点(2,1),则
的图象经过点(2,1),则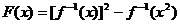 的值域为
的值域为
A.[2,5] B.[1,+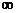 ] C.[2,10] D.[2,13]
] C.[2,10] D.[2,13]
 12.定义在R上的函数
12.定义在R上的函数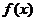 满足
满足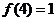 .
.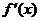 为
为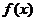 的导函数,已知函数
的导函数,已知函数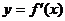 的图象如右图所示.若两正数
的图象如右图所示.若两正数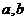 满足
满足 ,则
,则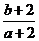 的取值范围是
的取值范围是
A.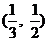 B.
B.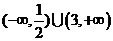 C.
C.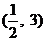 D.
D.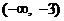
二.填空题:(每小题4分,共16分)
13.已知函数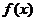 是奇函数,当
是奇函数,当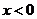 时,
时,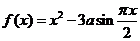 ,且
,且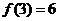 ,则实数
,则实数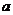 =__________.
=__________.
14.设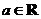 ,函数
,函数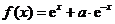 的导函数是
的导函数是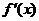 ,且
,且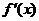 是奇函数 . 若曲线
是奇函数 . 若曲线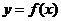 的一条切线的斜率是
的一条切线的斜率是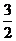 ,则切点的横坐标为______.
,则切点的横坐标为______.
15.设函数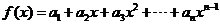 ,
,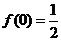 ,数列
,数列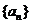 满足
满足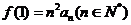 ,则数列
,则数列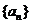 的通项
的通项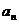 等于
.
等于
.
16.下列命题:
① 函数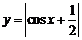 的最小正周期是
的最小正周期是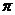 ;
;
②函数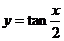 的图像的对称中心是
的图像的对称中心是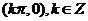 ;
;
③ 函数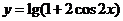 的递减区间是[
的递减区间是[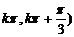
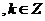 ;
;
④ 函数 的图像可由函数
的图像可由函数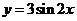 的图像按向量
的图像按向量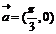 平移得到。其中正确的命题序号是 。
平移得到。其中正确的命题序号是 。
13
14
15
16
三.解答题:
17.(12分)已知△ABC的面积S满足3≤S≤3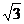 且
且 的夹角为
的夹角为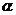 ,
,
(Ⅰ)求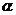 的取值范围;
的取值范围;
(Ⅱ)求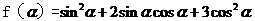 的最小值。
的最小值。
18. (12分)奥运会乒乓球比赛将产生男子单打、女子单打、男子团体、女子团体共四枚金牌,保守估计中国乒乓球男队获得每枚金牌的概率均为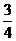 ,中国乒乓球女队获得一枚金牌的概率均为
,中国乒乓球女队获得一枚金牌的概率均为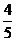 。
。
(I)求按此估计中国乒乓球女队比中国乒乓球男队多获得一枚金牌的概率;
(II)记中国乒乓球队获得金牌的数为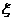 ,按此估计
,按此估计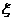 的分布列和数学期望
的分布列和数学期望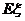 。
。
 19. (12分)已知斜三棱柱
19. (12分)已知斜三棱柱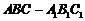 ,
,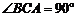 ,
,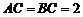 ,
,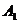 在底面
在底面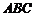 上的射影恰为
上的射影恰为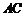 的中点
的中点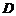 ,又知
,又知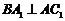 .
.
(Ⅰ)求证: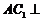 平面
平面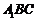 ;
;
(Ⅱ)求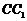 到平面
到平面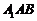 的距离;
的距离;
(Ⅲ)求二面角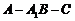 的大小.
的大小.
(1)求证:数列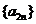 与
与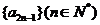 都是等比数列;
都是等比数列;
(2)求数列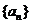 前
前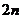 的和
的和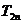 ;
;
(3)若数列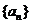 前
前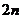 的和为
的和为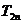 ,不等式
,不等式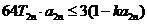 对
对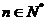 恒成立,求
恒成立,求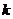 的最大值。
的最大值。
21. (12分)已知函数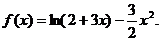
(I)求f(x)在[0,1]上的极值;
(II)若对任意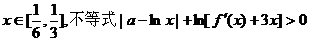 成立,求实数
成立,求实数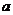 的取值范围;
的取值范围;
(III)若关于x的方程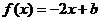 在[0,1]上恰有两个不同的实根,求实数b的取值范围.
在[0,1]上恰有两个不同的实根,求实数b的取值范围.
22. (14分)已知函数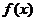 的定义域为
的定义域为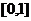 ,且同时满足:对任意
,且同时满足:对任意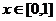 ,总有
,总有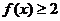 ,
,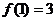 ; 若
; 若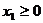 ,
,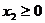 且
且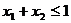 ,则有
,则有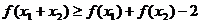 .
.
(I)求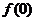 的值;
的值;
(II)试求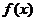 的最大值;
的最大值;
(III)设数列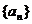 的前
的前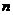 项和为
项和为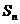 ,且满足
,且满足 ,
,
求证: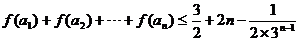 .
.
高2009级一诊模拟(理科)数学试题参考解答
一.选择题:
1.B.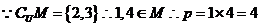
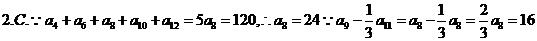
3.D.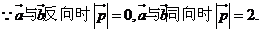
4.B.坐法有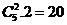
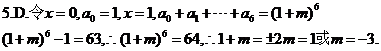
6. A.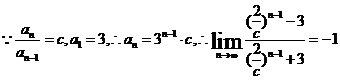
7.D. 由已知得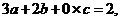 即
即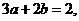
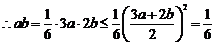
8.C.
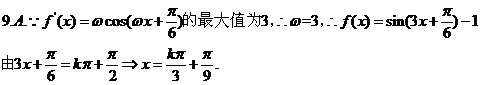
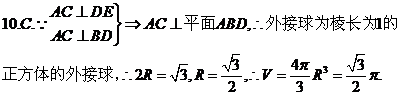
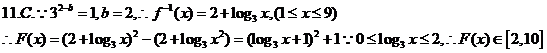
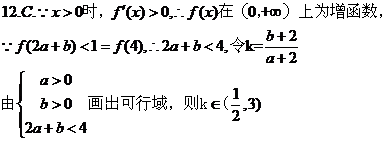
二.填空题:
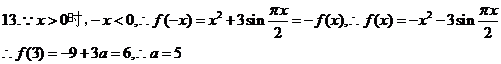
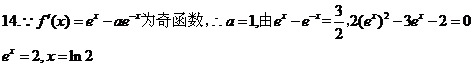
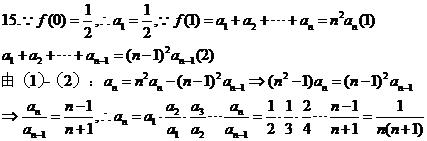
16. ②③.①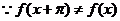 不正确;
不正确;
②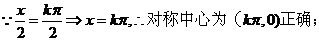
③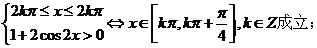
④应按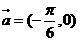 平移,所以不正确.
平移,所以不正确.
三.解答题:
17.解(Ⅰ)由题意知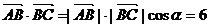
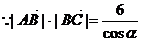
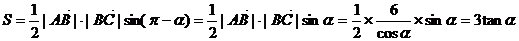
……………………3分
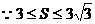
 ……………………4分
……………………4分
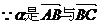 的夹角
的夹角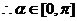
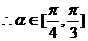 ……………………6分
……………………6分
(Ⅱ)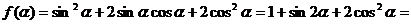
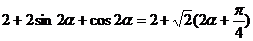 ……………………9分
……………………9分
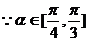
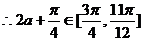
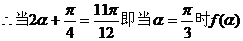 有最小值。
有最小值。
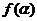 的最小值是
的最小值是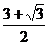 ……………………12分
……………………12分
18.(1)设中国乒乓球男队获0枚金牌,女队获1枚金牌为事件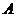 ,中国乒乓球男队获1枚金牌,女队获2枚金牌为事件
,中国乒乓球男队获1枚金牌,女队获2枚金牌为事件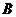 ,那么,
,那么,
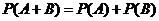 =
=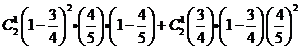 =
=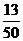
(2)根据题意中国乒乓球队获得金牌数是一随机变量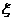 ,它的所有可能取值为0,1,2,3,4(单位:枚)
,它的所有可能取值为0,1,2,3,4(单位:枚)
那么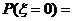
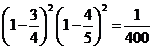
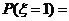
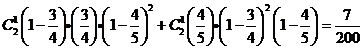
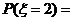
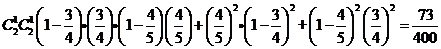
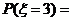
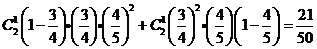
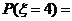
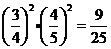 ……………………………………………………(8分)
……………………………………………………(8分)
则概率分布为:
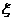
0
1
2
3
4

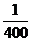
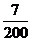
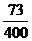
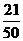
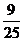
…………………………………………………………………(10分)
那么,所获金牌的数学期望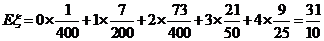 (枚)
(枚)
答:中国乒乓球队获得金牌数的期望为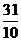 枚。……………………………….(12分)
枚。……………………………….(12分)
19. 解法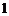 :(Ⅰ)∵
:(Ⅰ)∵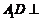 平面
平面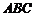 ,∴平面
,∴平面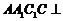 平面
平面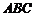 ,
,
又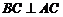 ,∴
,∴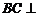 平面
平面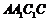 , 得
, 得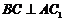 ,又
,又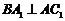 ,
,
 ∴
∴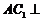 平面
平面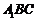 .…………………4分
.…………………4分
(Ⅱ)∵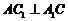 ,四边形
,四边形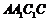 为菱形,故
为菱形,故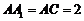 ,
,
又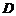 为
为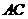 中点,知∴
中点,知∴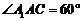 .取
.取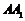 中点
中点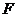 ,则
,则
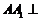 平面
平面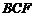 ,从而面
,从而面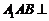 面
面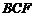 ,…………6分
,…………6分
过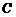 作
作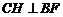 于
于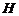 ,则
,则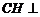 面
面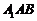 ,在
,在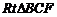 中,
中,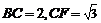 ,故
,故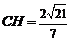 ,即
,即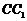 到平面
到平面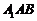 的距离为
的距离为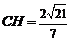 .…………………8分
.…………………8分
(Ⅲ)过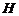 作
作 于
于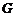 ,连
,连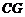 ,则
,则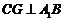 ,从而
,从而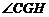 为二面角
为二面角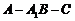 的平面角,在
的平面角,在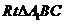 中,
中, ,∴
,∴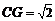 ,…………10分
,…………10分
在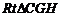 中,
中,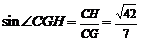 ,故二面角
,故二面角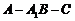 的大小为
的大小为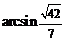 .
.
…………………12分
 解法
解法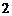 :(Ⅰ)如图,取
:(Ⅰ)如图,取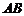 的中点
的中点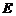 ,则
,则 ,∵
,∵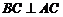 ,∴
,∴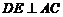 ,
,
又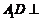 平面
平面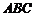 ,以
,以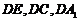 为
为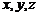 轴建立空间坐标系, …………1分
轴建立空间坐标系, …………1分
则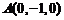 ,
,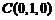 ,
,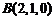 ,
,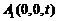 ,
,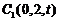 ,
,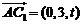 ,
,
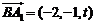 ,
,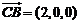 ,由
,由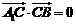 ,知
,知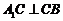 ,
,
又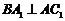 ,从而
,从而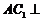 平面
平面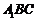 .…………………4分
.…………………4分
(Ⅱ)由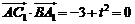 ,得
,得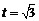 .设平面
.设平面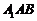 的法向量
的法向量
为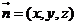 ,
,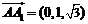 ,
,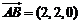 ,
,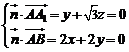 ,
,
设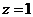 ,则
,则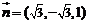 .…………6分
.…………6分
∴点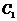 到平面
到平面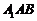 的距离
的距离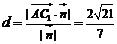 .…………………8分
.…………………8分
(Ⅲ)设面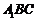 的法向量为
的法向量为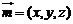 ,
,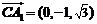 ,
,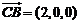 ,
,
∴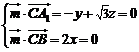 .…………10分
.…………10分
设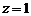 ,则
,则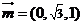 ,故
,故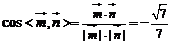 ,根据法向量的方向
,根据法向量的方向
可知二面角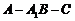 的大小为
的大小为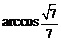 .…………………12分
.…………………12分
20. 解:(1)∵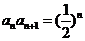 ,∴
,∴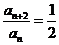 2分
2分
∴数列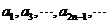 是以1为首项,
是以1为首项,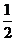 为公比的等比数列;
为公比的等比数列;
(2)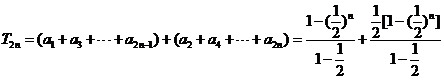
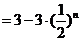 9分
9分
(3)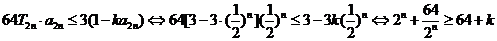
21. 解:(I)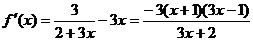 ,
,
令 (舍去)
(舍去)
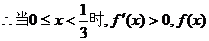 单调递增;
单调递增;
当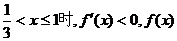 单调递减.
单调递减.
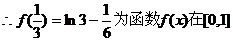 上的极大值
上的极大值
(II)由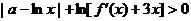 得
得
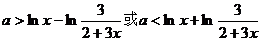 , …………①
, …………①
设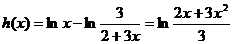 ,
,
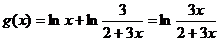 ,
,
依题意知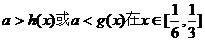 上恒成立,
上恒成立,
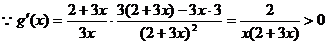 ,
,
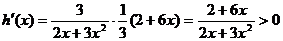 ,
,
 上单增,要使不等式①成立,
上单增,要使不等式①成立,
当且仅当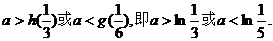
(III)由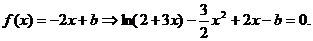
令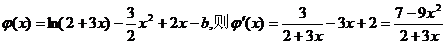 ,
,
当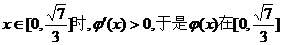 上递增;
上递增;
当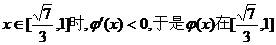 上递减
上递减
而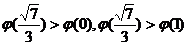 ,
,
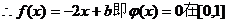 恰有两个不同实根等价于
恰有两个不同实根等价于
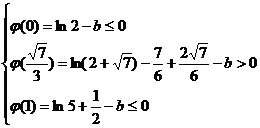
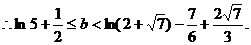
22.解:(1)令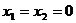 ,则
,则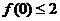 ,又由题意,有
,又由题意,有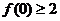
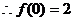 …………………3分
…………………3分
(2)任取 且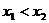 ,则0<
,则0<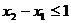
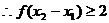
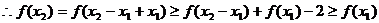
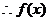 的最大值为
的最大值为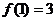 …………………6分
…………………6分
(3)由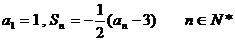
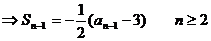
又由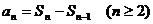
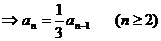
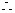 数列
数列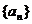 为首项为1,公比为
为首项为1,公比为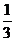 的等比数列,
的等比数列, 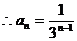 ………8分
………8分
当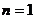 时,
时,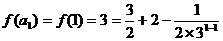 ,不等式成立,
,不等式成立,
当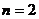 时,
时,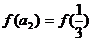
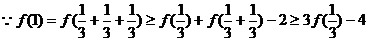 ,
, 
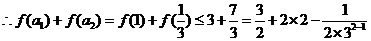 不等式成立
不等式成立
假设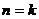 时,不等式成立。
时,不等式成立。
即 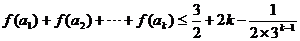
则 当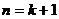 时,
时,
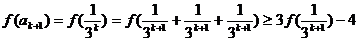
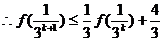
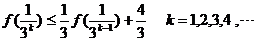
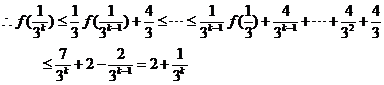
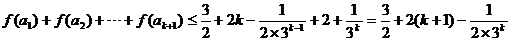
即 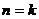 时,不等式成立
时,不等式成立
故
对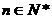 ,原不等式成立。
……………14分
,原不等式成立。
……………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com