
2009届高考数学第三轮复习精编模拟五
参考公式:
如果事件 互斥,那么
球的表面积公式
互斥,那么
球的表面积公式


如果事件 相互独立,那么
其中
相互独立,那么
其中 表示球的半径
表示球的半径
 球的体积公式
球的体积公式
如果事件 在一次试验中发生的概率是
在一次试验中发生的概率是 ,那么
,那么

 次独立重复试验中事件
次独立重复试验中事件 恰好发生
恰好发生 次的概率
其中
次的概率
其中 表示球的半径
表示球的半径

第一部分 选择题(共50分)
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的
1、设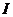 为全集,
为全集,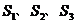 是
是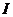 的三个非空子集,且
的三个非空子集,且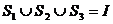 ,则下面论断正确的是 ( )w.w.w.k.s.5.u.c.o.m
,则下面论断正确的是 ( )w.w.w.k.s.5.u.c.o.m
(A)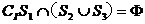 ; (B)
; (B)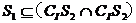 ;
;
 (C)
(C)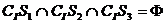 ;(D)
;(D) .
.
2、已知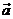 、
、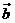 是非零向量且满足(
是非零向量且满足(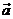 -2
-2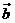 ) ⊥
) ⊥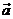 ,(
,(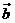 -2
-2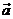 ) ⊥
) ⊥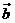 ,则
,则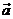 与
与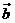 的夹角是 ( )
的夹角是 ( )
(A).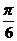 (B)
(B) 
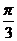 (C).
(C).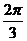 (D).
(D).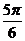
3、已知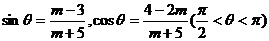 ,则
,则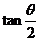 等于 ( )
等于 ( )
A、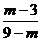 B、
B、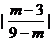 C、
C、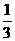 D、
D、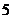
4、已知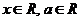 ,
,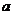 为常数,且
为常数,且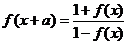 ,则函数
,则函数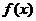 必有一周期为: ( )
必有一周期为: ( )
A、2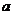 B、
B、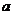 C、4
C、4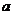 D、5
D、5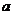
5、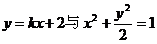 交于A、B两点,且
交于A、B两点,且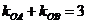 ,则直线AB的方程为: ( )
,则直线AB的方程为: ( )
A、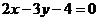 B、
B、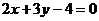
C、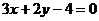 D、
D、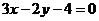
6、我国储蓄存款采取实名制并征收利息税,利息税由各银行储蓄点代扣代收。某人在2001年9月存入人民币1万元,存期一年,年利率为2.25%,到期时净得本金和利息共计10180元,则利息税的税率是: ( )
A、8% B、20% C、32% D、80%
7、不等式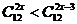 的解集是( )
的解集是( )
A、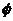 B、
B、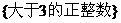 C、{4,5,6} D、{4,4.5,5,5.5,6}
C、{4,5,6} D、{4,4.5,5,5.5,6}
8、七人并排站成一行,如果甲、乙两人必需不相邻,那么不同的排法的种数是( )
(A) 1440 (B) 3600 (C) 4320 (D) 4800
9、若关于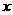 的方程
的方程 只有一个实数根,则
只有一个实数根,则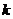 的取值范围为( )
的取值范围为( )
A、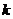 =0
B、
=0
B、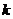 =0或
=0或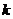 >1
>1
C、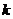 >1或
>1或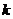 <-1 D、
<-1 D、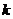 =0或
=0或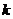 >1或
>1或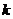 <-1
<-1
10、一个四面体的所有棱长都为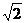 ,四个项点在同一球面上,则此球的表面积为( )
,四个项点在同一球面上,则此球的表面积为( )
(A)3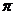 (B)4
(B)4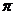 (C)3
(C)3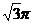 (D)6
(D)6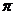
第二部分 非选择题(共100分)
二、填空题:本大题共5小题,其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.每小题5分,满分20分.
11、已知函数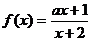 在区间
在区间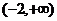 上为增函数,则实数a的取值范围是 。
上为增函数,则实数a的取值范围是 。
12、有些计算机对表达式的运算处理过程实行“后缀表达式”:运算符号紧跟在运算对象的后面,按照从左到右的顺序运算,如表达式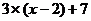 ,其运算为:
,其运算为: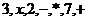 ,若计算机进行运算:
,若计算机进行运算: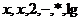 ,那么使此表达式有意义的
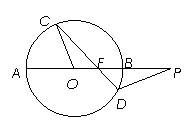
,那么使此表达式有意义的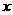 的范围为 _____________ .
的范围为 _____________ .
13、若四面体各棱的长是1或2,且该四面体不是正四面体,则其体积是 (只需写出一个可能的值).
 14、(坐标系与参数方程选做题)
极坐标系中,点P
14、(坐标系与参数方程选做题)
极坐标系中,点P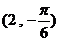 到直线:
到直线: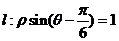 的距离是 .
的距离是 .
15.(几何证明选讲选做题) 如图,圆 O 的割线 PBA 过圆心 O,弦 CD 交 PA 于点F,且△COF∽△PDF,PB = OA = 2,则PF = 。
三.解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
已知命题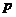 :方程
:方程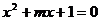 有两个不等的负实根;
有两个不等的负实根;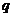 :方程
:方程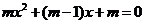 无实根.若“
无实根.若“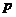 或
或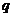 ”为真,“
”为真,“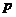 且
且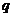 ”为假,求实数
”为假,求实数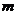 的取值范围.
的取值范围.
17.(本小题满分12分)
在△ABC中,已知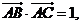
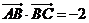 .
.
(1) 求AB边的长度;
(2) 证明:
证明: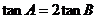 ;
;
(3)若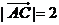 ,求
,求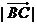 .
.
18.(本小题满分14分)
已知函数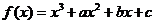 图像上一点
图像上一点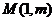 处的切线方程为
处的切线方程为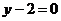 ,其中
,其中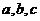 为常数.
为常数.
(Ⅰ)函数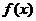 是否存在单调减区间?若存在,则求出单调减区间(用
是否存在单调减区间?若存在,则求出单调减区间(用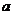 表示);
表示);
(Ⅱ)若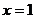 不是函数
不是函数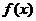 的极值点,求证:函数
的极值点,求证:函数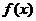 的图像关于点
的图像关于点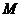 对称.
对称.
19.(本小题满分14分)
SD垂直于底面ABCD,SB=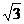 .
.
(I)求证BC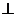 SC;
SC;
(II)求面ASD与面BSC所成二面角的大小;
(III)设棱SA的中点为M,求异面直线DM与SB所成角的大小.
20.(本小题满分14分)
设圆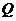 过点P(0,2), 且在
过点P(0,2), 且在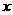 轴上截得的弦RG的长为4.
轴上截得的弦RG的长为4.
(1)求圆心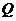 的轨迹E的方程;
的轨迹E的方程;
21.(本小题满分14分)
在平面直角坐标系上,设不等式组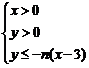 (
(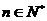 )
)
所表示的平面区域为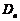 ,记
,记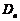 内的整点(即横坐标和纵坐标均
内的整点(即横坐标和纵坐标均
(Ⅰ)求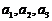 并猜想
并猜想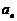 的表达式再用数学归纳法加以证明;
的表达式再用数学归纳法加以证明;
(Ⅱ)设数列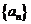 的前
的前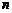 项和为
项和为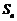 ,数列
,数列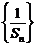 的前
的前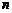 项和
项和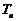
 ,
,
是否存在自然数m?使得对一切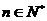 ,
,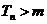 恒成立。若存在,
恒成立。若存在,
求出m的值,若不存在,请说明理由。
一.选择题:CBDCC BDBDA
解析:1: 由文氏图可得结论(C).
2:由已知得:( -2
-2 )
)
 =0,(
=0,( -2
-2 )
)
 =0;即得:
=0;即得: =
= =2
=2

 ,∴cos<
,∴cos< ,
, >=
>= ,∴选(B)
,∴选(B)
3:由于受条件sin2θ+cos2θ=1的制约,故m为一确定的值,于是sinθ,cosθ的值应与m的值无关,进而推知tan 的值与m无关,又
的值与m无关,又 <θ<π,
<θ<π, <
< <
< ,∴tan
,∴tan >1,故选D。
>1,故选D。
4:由于 ,从而函数
,从而函数 的一个背景为正切函数tanx,取
的一个背景为正切函数tanx,取 ,可得必有一周期为4
,可得必有一周期为4 。故选C。
。故选C。
5:解此题具有很大的迷惑性,注意题目隐含直线AB的方程就是 ,它过定点(0,2),只有C项满足。故选C。
,它过定点(0,2),只有C项满足。故选C。
6:生活常识告诉我们利息税的税率是20%。故选B。
7:四个选项中只有答案D含有分数,这是何故?宜引起高度警觉,事实上,将x值取4.5代入验证,不等式成立,这说明正确选项正是D,而无需繁琐地解不等式。
8:(用排除法)七人并排站成一行,总的排法有 种,其中甲、乙两人相邻的排法有2×
种,其中甲、乙两人相邻的排法有2× 种.因此,甲、乙两人必需不相邻的排法种数有:
种.因此,甲、乙两人必需不相邻的排法种数有: -2×
-2× =3600,对照后应选B;
=3600,对照后应选B;
 9:作直线
9:作直线 的图象和半圆
的图象和半圆 ,从图中可以看出:
,从图中可以看出:  的取值范围应选(D).
的取值范围应选(D).
注:求与方程实数根个数有关的问题常用图解法.
 10:如图,将正四面体ABCD补形成正方体,则正四面体、正方体的中心与其外接球的球心共一点.因为正四面体棱长为
10:如图,将正四面体ABCD补形成正方体,则正四面体、正方体的中心与其外接球的球心共一点.因为正四面体棱长为 ,所以正方体棱长为1,从而外接球半径R=
,所以正方体棱长为1,从而外接球半径R= .故S球=3
.故S球=3 .
.
二.填空题:11、 ; 12、
; 12、 ; 13、
; 13、 或
或 或
或 ;
;
14、+1; 15、3;
解析:11: ,由复合函数的增减性可知,
,由复合函数的增减性可知, 在
在 上为增函数,∴
上为增函数,∴ ,∴
,∴ 。
。
12:计算机进行运算: 时,它表示的表达式是
时,它表示的表达式是 ,当其有意义时,得
,当其有意义时,得 ,解得
,解得 .
.
13: 本题是一道很好的开放题,解题的开窍点是:每个面的三条棱是怎样构造的,依据“三角形中两边之和大于第三边”,就可否定{1,1,2},从而得出{1,1,1},{1,2,2},{2,2,2}三种形态,再由这三类面构造满足题设条件的四面体,最后计算出这三个四面体的体积分别为:
 ,
, ,
, ,故应填.
,故应填. 、
、 、
、 中的一个即可.
中的一个即可.
14.解:直线: 化为一般方程:
化为一般方程: ,点P
,点P 化为点
化为点 ,则点
,则点 到直线的距离为
到直线的距离为
15解:由△COF∽△PDF得 ,即
,即 =
=
= =
= ,即
,即 =
= ,
,
解得 ,故
,故 =3
=3
三.解答题:
16.解:当P为真时,有 ……4分
……4分
当Q为真时,有 ……5分
……5分
 ……6分
……6分
由题意:“P或Q”真,“P且Q”为假 等价于
(1)P真Q假: ……8分
……8分
(2)Q真P假: ……11分
……11分
综合(1)(2) 的取值范围是
的取值范围是 ……12分
……12分
17.解:(1)∵ ∴
∴
∵ ∴
∴ ,
,  即AB边的长度为
即AB边的长度为 ……………………3分
……………………3分
(2) 由 得
得 -------------①
-------------①
 即
即 -------------②
-------------②
由①②得 , 由正弦定理得
, 由正弦定理得
∴ ∴
∴ -- ……………………8分
-- ……………………8分
(3) ∵ ,由(2)中①得
,由(2)中①得 由余弦定理得
由余弦定理得 =
=
∴ =
= - ……………………12分
- ……………………12分
18.解:(Ⅰ) ,
, , ……………1分
, ……………1分
由题意,知 ,
,
 ,
,
即 ……………………2分
……………………2分
 …………………3分
…………………3分
①
当 时,
时, ,函数
,函数 在区间
在区间 上单调增加,
上单调增加,
不存在单调减区间; ……………………5分
②
当 时,
时, ,有
,有





+
-
+




 当
当 时,函数
时,函数 存在单调减区间,为
存在单调减区间,为 ……………7分
……………7分
③
当 时,
时,  ,有
,有





+
-
+




 当
当 时,函数
时,函数 存在单调减区间,为
存在单调减区间,为 …………9分
…………9分
(Ⅱ)由(Ⅰ)知:若 不是函数
不是函数 的极值点,则
的极值点,则 ,
,

 …………………10分
…………………10分
设点 是函数
是函数 的图像上任意一点,则
的图像上任意一点,则 ,
,
点 关于点
关于点 的对称点为
的对称点为 ,
,

(或  )
)
 点
点 在函数
在函数 的图像上.
的图像上.
 由点
由点 的任意性知函数
的任意性知函数 的图像关于点
的图像关于点 对称.
…………………14分
对称.
…………………14分
19. [方法一]:(几何法)
(I)证法一:如图1,∵底面ABCD是正方形, ∴BC⊥DC.
∵SD⊥底面ABCD,∴DC是SC在平面ABCD上的射影,
由三垂线定理得BC⊥SC. …………3分
证法二:如图1,∵底面ABCD是正方形, ∴BC⊥DC.
∵SD⊥底面ABCD,∴SD⊥BC,又DC∩SD=D, 图1
∴BC⊥平面SDC,∴BC⊥SC. …………3分
(II)解法一:∵SD⊥底面ABCD,且ABCD为正方形,
 ∴可把四棱锥S―ABCD补形为长方体A1B1C1S―ABCD,
∴可把四棱锥S―ABCD补形为长方体A1B1C1S―ABCD,
如图2,面ASD与面BSC所成的二面角就是面ADSA1与面BCSA1所成的二面角,
∵SC⊥BC,BC//A1S, ∴SC⊥A1S,
又SD⊥A1S,∴∠CSD为所求二面角的平面角.
在Rt△SCB中,由勾股定理得SC= ,在Rt△SDC中,
,在Rt△SDC中,
由勾股定理得SD=1.
∴∠CSD=45°.即面ASD与面BSC所成的二面角为45°. ……………8分
解法二:如图3,过点S作直线
 在面ASD上,
在面ASD上,
∵底面ABCD为正方形, 在面BSC上,
在面BSC上,

∴∠CSD为面ASD与面BSC所成二面角的平面角.
在Rt△SCB中,由勾股定理得SC= ,在Rt△SDC中,
,在Rt△SDC中,
由勾股定理得SD=1.
∴∠CSD=45°.即面ASD与面BSC所成的二面角
为 45°。…8分
(III)解法一:如图3, ∵SD=AD=1,∠SDA=90°, ∴△SDA是等腰直角三角形.
又M是斜边SA的中点, ∴DM⊥SA.
∵BA⊥AD,BA⊥SD,AD∩SD=D,∴BA⊥面ASD,SA是SB在面ASD上的射影.
由三垂线定理得DM⊥SB. ∴异面直线DM与SB所成的角为90°. ……………14分
在△ABS中,由中位线定理得 MP//SB, 是异面直线DM与SB所成的角.
是异面直线DM与SB所成的角.
 ,
,
又
∴在△DMP中,有DP2=MP2+DM2, 
即异面直线DM与SB所成的角为90°. ……………14分
解析:如图所示,以D为坐标原点建立直角坐标系,
则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),
M( ,0,
,0, ),
),
∵ SB= ,DB=
,DB= ,SD=1,∴ S(0,0,1),……………2分
,SD=1,∴ S(0,0,1),……………2分
(I)证明:∵  ,
,

 =0 ∴
=0 ∴  ,即BC
,即BC SC.……………5分
SC.……………5分
(II)设二面角的平面角为θ,由题意可知平面ASD的一个法向量为 ,设平面BSC的法向量为
,设平面BSC的法向量为 ,由
,由


 ,
,
得
 ,
,
∴ 面ASD与面BSC所成的二面角为45°.……………10分
(III)设异面直线DM与SB所成角为α,
 ∵
∵  ,SB=(-1,-1,1),得
,SB=(-1,-1,1),得

∴ 异面直线DM与SB所成角为90°.……………14分

20.解:(1)设圆心 的坐标为
的坐标为 ,如图过圆心
,如图过圆心 作
作 轴于H,
轴于H,
则H为RG的中点,在 中,
中, …3分
…3分
∵ ∴
∴
即 …………………6分
…………………6分
(2) 设 ,
,
直线AB的方程为 (
( )则
)则 -----①
-----① ---②
---②
∵点 在直线
在直线 上, ∴
上, ∴ .
.
∴点M的坐标为 . ………………10分
. ………………10分
同理可得: ,
,  ,
,
∴点 的坐标为
的坐标为 . ………………11分
. ………………11分
直线 的斜率为
的斜率为 ,其方程为
,其方程为
 ,整理得
,整理得 ,………………13分
,………………13分
显然,不论 为何值,点
为何值,点 均满足方程,
均满足方程,
∴直线 恒过定点
恒过定点 .……………………14分
.……………………14分
21.解:(Ⅰ)当n=1时,D1为Rt△OAB1的内部包括斜边,这时
 ,
,
当n=2时,D2为Rt△OAB2的内部包括斜边,这时
 ,
,
当n=3时,D3为Rt△OAB3的内部包括斜边,这时
 ,……, ---3分
,……, ---3分
 由此可猜想
由此可猜想 =3n。
--------------------------------------------------4分
=3n。
--------------------------------------------------4分
下面用数学归纳法证明:
(1) 当n=1时,猜想显然成立。
(2) 假设当n=k时,猜想成立,即 ,(
,( ) ----5分
) ----5分
如图,平面区域 为Rt
为Rt 内部包括斜边、平面区域
内部包括斜边、平面区域 为
为
Rt△ 内部包括斜边,∵平面区域
内部包括斜边,∵平面区域 比平面区域
比平面区域 多3
多3
个整点, ------- 7分
即当n=k+1时, ,这就是说当n=k+1时,
,这就是说当n=k+1时,
猜想也成立,
由(1)、(2)知 =3n对一切
=3n对一切 都成立。 ---------------------8分
都成立。 ---------------------8分
(Ⅱ)∵ =3n, ∴数列
=3n, ∴数列 是首项为3,公差为3的等差数列,
是首项为3,公差为3的等差数列,
∴ .
.
 -------------------------10分
-------------------------10分


= =
= -------------------------------11分
-------------------------------11分
∵对一切 ,
, 恒成立, ∴
恒成立, ∴
∵ 在
在 上为增函数 ∴
上为增函数 ∴ ---13分
---13分
 ,满足
,满足 的自然数为0,
的自然数为0,
∴满足题设的自然数m存在,其值为0。 -------------------------14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com