
杭州学军中学高三年级2006学年第三次月考
数学试卷(问卷)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合A={1,2}, 则满足 的集合B的个数是
( )
的集合B的个数是
( )
A. 1 B.
2.设函数 的反函数为
的反函数为 ,且
,且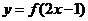 的图象过点
的图象过点 ,则
,则 的图象必过点……………………………………………………………( )
的图象必过点……………………………………………………………( )
A. B.
B. 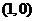 C.
C. 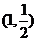 D.
D.
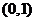
3.若不等式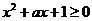 对一切
对一切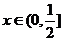 成立,则
成立,则 的最小值为…………( )
的最小值为…………( )
A.0 B.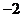 C.
C.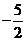 D.
D.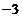
4.如果随机变量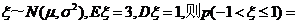 …………………( )A.
…………………( )A.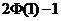 B.
B.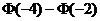 C.
C. 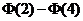 D.
D. 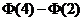
5.函数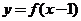 的图象如右图所示,
的图象如右图所示,
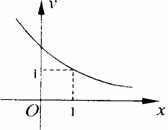 它在R上单调递减.现有如下结论:
它在R上单调递减.现有如下结论:
①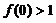 ;②
;②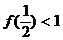 ;
;
③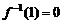 ;④
;④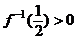
其中正确结论的个数是………( ) ( )
A.1 B.2
C.3 D.4
6.下列命题:①若极限 存在,则函数
存在,则函数 在
在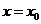 处连续的逆命题;②若
处连续的逆命题;②若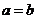 ,则
,则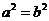 的否命题;③若“p或q为真命题”,则“p且q为真命题”的逆否命题,其中真命题的个数是……………………………………………………(
)
的否命题;③若“p或q为真命题”,则“p且q为真命题”的逆否命题,其中真命题的个数是……………………………………………………(
)
A. 0个 B. 1个 C. 2个 D. 3个
7.设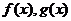 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当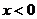 时,
时,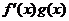
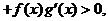 且
且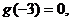 则不等式
则不等式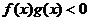 的解集是…………( )
的解集是…………( )
A. B.
B.
C. D.
D.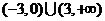
8.函数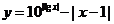 的图象大致是…………………………………………( )
的图象大致是…………………………………………( )

9.复数z=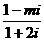 (i为虚数单位)在复平面上对应的点一定不位于……………(
)
(i为虚数单位)在复平面上对应的点一定不位于……………(
)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10、已知等差数列{an}的前n项和为Sn,若
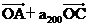 ,且A、B、C三点共线(该直线不过原点O),则S200=………………………………………………( )
,且A、B、C三点共线(该直线不过原点O),则S200=………………………………………………( )
A.100
B.
二、填空题:本大题共4个小题;每小题4分,共16分.
11.某校对全校男女学生共1200名进行健康调查,选用分层抽样法抽取一个容量为200的样本.已知男生比女生多抽了10人,则该校的男生人数应是 .
12.用数学归纳法证明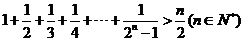 时,假设
时,假设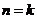 成立,当
成立,当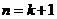 时,左端增加的项有______项。
时,左端增加的项有______项。
13.已知数列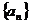
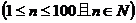 满足:数列
满足:数列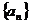 中任一项
中任一项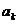 比其余99项之和小k,则
比其余99项之和小k,则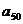 = .
= .
14.设函数 ,则下列判断中正确的是 (填上序号)
,则下列判断中正确的是 (填上序号)
①函数 为偶函数; ②若
为偶函数; ②若 ,则
,则 ;
;
③函数 在
在 上为单调增函数;④若
上为单调增函数;④若 ,则
,则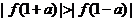

 杭州学军中学高三年级2006学年第三次月考
杭州学军中学高三年级2006学年第三次月考
座位号
数学试卷答卷
一、选择题:本大题共10个小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题:本大题共4个小题,每小题4分,共16分.
11. 12.
13. 14.
三、解答题:本大题共6个小题,每小题14分,共84分.
15.已知命题P: ,命题Q:
,命题Q: ,若命题P是命题Q的一个充分而不必要条件,求实数m的取值范围.
,若命题P是命题Q的一个充分而不必要条件,求实数m的取值范围.
16.甲、乙、丙三人独立回答同一道数学问题,其中任何一人答对与否,对其它人答题结果无影响.已知甲答对的概率为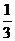 ,乙、丙答对的概率均为
,乙、丙答对的概率均为 ,设有
,设有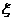 人答对此题,请写出随机变量
人答对此题,请写出随机变量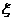 的概率分布及期望.
的概率分布及期望.
 17.在直三棱柱
17.在直三棱柱 中,底面三角形ABC是直角三角形,
中,底面三角形ABC是直角三角形,
截面 与截面
与截面 交于DE,
交于DE,
(1)求证: ;
;
(2)求证: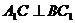 ;
;
(3)求证:DE//平面ABC;
(4)设二面角 。
。
18.已知函数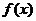 =
=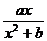 ,若
,若 且
且 ,
,
(1)求函数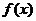 的解析式;
的解析式;
(2)若 为
为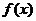 =
=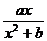 图象上的任意一点,直线
图象上的任意一点,直线 与
与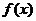 =
=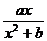 的图象切于
的图象切于 点,求直线
点,求直线 的斜率的取值范围.
的斜率的取值范围.
19.设 而
而 是方程
是方程 的两根。
的两根。
(1)记 ,求证数列
,求证数列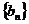 等差数列,并求出其首项和公差;
等差数列,并求出其首项和公差;
(2)求证:对任意正整数n都有: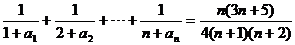
20.设函数 的定义域为R,对于任意实数
的定义域为R,对于任意实数 ,总有
,总有
且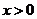 时,
时, ,
,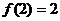
(1)证明: 是奇函数;
是奇函数;
(2)证明: 在R上单调递增;
在R上单调递增;
(3)设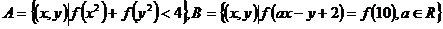 ,
,
若 ,试确定
,试确定 的取值范围.
的取值范围.
一、选择题:本大题共10个小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
C
B
C
D
C
B
A
D
B
A
二、填空题:本大题共4个小题,每小题4分,共16分.
11. 630 12. 2k 13.  14. ①②③
14. ①②③
三、解答题:本大题共6个小题,每小题14分,共84分.
15. (4分)
(4分) 
由题意得

16.  有分布列:
有分布列:

0
1
2
3
P




从而期望
17.(1)
又

(2) 


(3)DE//AB,
(4)设BB1的中点为F,连接EF、DF,则EF是DF在平面BB
因为BB

18.(1) 由题意得

(2) 
所以直线 的斜率为
的斜率为
令 ,则直线
,则直线 的斜率
的斜率 ,
,
19.(1)由韦达定理得


 是首项为4,公差为2的等差数列。
是首项为4,公差为2的等差数列。
(2)由(1)知 ,则
,则
原式左边=
= =右式。故原式成立。
=右式。故原式成立。
20.令x=y=0,有 ,令y=-x则
,令y=-x则 得
得
故(1)得证。
(2)在R上任取x1,x2且 ,且
,且 ,
,

所以 在R上单调递增;
在R上单调递增;
(3)
由
 得
得 ;
;
由 得
得 ;因为
;因为 ,
,
所以 无解,即圆心到直线的距离大于或等于半径2,只需
无解,即圆心到直线的距离大于或等于半径2,只需

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com