
咸阳市2009年高考模拟考试试题
理 科 数 学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至3页。第Ⅱ卷3至8页。考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
注意事项:
1.答题前,考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚,并贴好条形码。请认真核准条形码上的准考证号、姓名和科目。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效。
3.本卷共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
参考公式:
如果事件 、
、 互斥,那么
球的表面积公式
互斥,那么
球的表面积公式


如果事件A、B相互独立,那么 其中R表示球的半径
 球的体积公式
球的体积公式
如果事件A在一次实验中发生的概率是P,那么
V=
n次独立重复试验中事件A恰好发生k次的概率 其中R表示球的半径
 (k=0,1,2,…,n)
(k=0,1,2,…,n)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 定义集合运算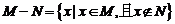 ,若
,若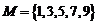 ,
,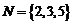 ,则
,则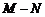 =
=
A.M
B.N
C.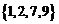 D.
D.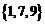
2. 复数 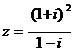 对应的点所位于的象限是
对应的点所位于的象限是
A. 一 B. 二 C. 三 D. 四
3.已知向量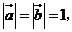 ,
,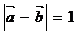 ,则
,则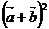 的值为
的值为
A. 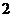 B.
B. 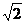 C.
C.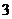 D.
D.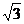
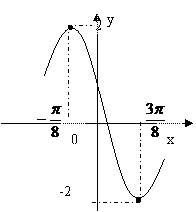 4.已知函数
4.已知函数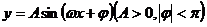
的一段图象如图,则函数的解析式为
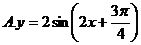
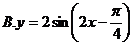
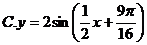
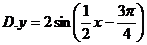
5.“等式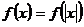 对
对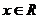 恒成立”是“函数
恒成立”是“函数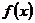 在
在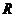 上为偶函数”的
上为偶函数”的
 充分不必要条件
充分不必要条件  必要不充分条件
必要不充分条件  充要条件
充要条件
 既不充分也不必要条件
既不充分也不必要条件
6. 在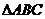 中,
中,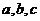 分别是内角
分别是内角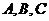 的对边,如果
的对边,如果 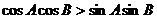 ,那么,三边
,那么,三边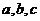 满足的关系是
满足的关系是
A. 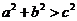 B.
B. 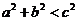 C.
C. 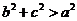 D.
D. 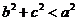
7. 已知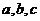 成等比数列,则函数
成等比数列,则函数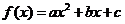 与
与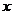 轴的交点个数是
轴的交点个数是
A. 0
B.
8.金太阳艺术小组有9人,每人至少会钢琴和小号中的1种乐器,其中7人会钢琴,3人会小号,现从中选出会钢琴和会小号的各1人,不同的选法种数是
A.10 B.1
9.设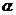 、
、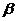 为两个不同的平面,
为两个不同的平面,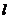 、
、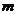 为两条不同的直线,且
为两条不同的直线,且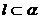 ,
,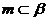 ,有如下的两个命题:①若
,有如下的两个命题:①若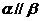 ,则
,则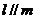 ;②若
;②若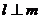 ,则
,则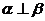 ;那么
;那么
A. ①是真命题,②是假命题 B. ①是假命题,②是真命题
C. ①、②都是真命题 D. ①、②都是假命题
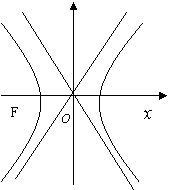




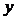




 10. 如图,双曲线
10. 如图,双曲线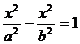 ,
,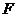 为左焦点,
为左焦点,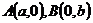 ,当
,当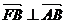 时,双曲线被称为“黄金双曲线”。则其离心率
时,双曲线被称为“黄金双曲线”。则其离心率 等于
等于
 A.
A. 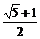 B.
B. 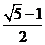 C.
C. 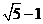 D .
D . 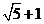
11.若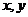 满足
满足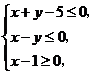 则
则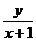 的取值范围为
的取值范围为
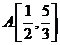
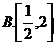

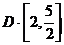
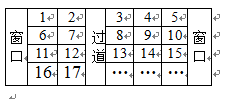 12.两旅客坐火车外出旅游,希望座位连在一起,且有一个靠窗,已知火车上的座位的排法如右图所示,则下列座位号码符合要求的应当是
12.两旅客坐火车外出旅游,希望座位连在一起,且有一个靠窗,已知火车上的座位的排法如右图所示,则下列座位号码符合要求的应当是
A. 48,49 B. 62,63
C. 75,76 D. 84,85
第Ⅱ卷
二、 填空题:本大题共4小题,每小题4分,共16分.将答案填在题中的横线上.
13. 若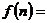
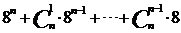
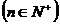 ,则
,则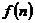 被9除所得的余数为 .
被9除所得的余数为 .
14. 单位正方体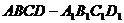 ,过
,过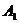 、
、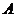 、
、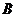 、
、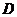 四点的球的表面积为 .
四点的球的表面积为 .
15. 若函数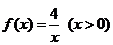 ,点P(x,y)在曲线
,点P(x,y)在曲线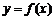 上运动,作PM垂直x轴于M,则△POM(O为坐标原点)周长的最小值是___________.
上运动,作PM垂直x轴于M,则△POM(O为坐标原点)周长的最小值是___________.
16.已知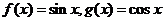 ,则有:
,则有: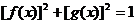 ,
, ,
,
 .若设:
.若设: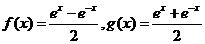 ,类比上例则可得到
,类比上例则可得到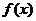 与
与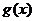 的关系式为________
____.(只须写出一种即可)
的关系式为________
____.(只须写出一种即可)
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
求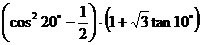 的值.
的值.
18.(本小题满分12分)
在一次考试中共有12道选择题,每道选择题都有4个选项,其中有且只有一个选项是正确的.评分标准规定:“每题只选一个选项,选对得5分,不选或选错得0分”.某考生已确定有8道题答案是正确的,其余题中:有两道只能分别判断2个选项是错误的,有一道仅能判断1个选项是错误的,还有一道因不理解题意只好乱猜,求:
(I)该考生得50分的概率;
(II)该考生所得分数的数学期望.
 19.(本小题满分12分)
19.(本小题满分12分)
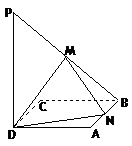
如图,正方形ABCD的边长为4,PD⊥平面ABCD,PD=6,M、N分别是PB、AB的中点.
(I)求证:MN⊥CD;
(II) 求二面角M-DN-C大小.
20.(本小题满分12分)
已知函数 与
与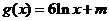 ,
,
(I)求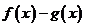 的单调区间;
的单调区间;
(II)若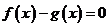 恰有两个不同的根,求实数
恰有两个不同的根,求实数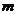 的值.
的值.
21.(本小题满分12分)
 已知在平面直角坐标系
已知在平面直角坐标系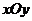 中的一个椭圆,它的中心在原点,左准线为
中的一个椭圆,它的中心在原点,左准线为 ,离心率
,离心率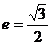 ,设点
,设点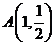 .
.
(I) 求该椭圆的标准方程;
(II) 过原点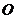 的直线交椭圆于点
的直线交椭圆于点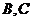 ,求
,求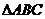 面积的最大值.
面积的最大值.
22.(本小题满分14分)
已知数列{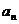 }满足
}满足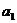 =2,
=2,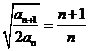 .
.
(I)求数列{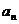 }的通项公式;
}的通项公式;
(II)设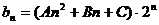 ,试推断是否存在常数A,B,C,使对一切
,试推断是否存在常数A,B,C,使对一切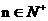 都有
都有
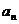 =
=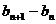 成立?若存在,求出A,B,C的值,若不存在,说明理由;
成立?若存在,求出A,B,C的值,若不存在,说明理由;
(III)求证: .
.
咸阳市2009年高考模拟考试试题(一)
一、选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
B
C
A
C
B
A
D
D
A/B
B
D
二、 填空题:
13. 8
14.(理) (文)
(文)
15. 
16. 或
或  或
或 
三、解答题: 答案仅供参考,其他解法参照给分
17.(本小题满分12分)
(理) 解:

(文) 解:(1)由两角和差公式及二倍角公式得

由 得
得

于是函数 的单调递增区间为
的单调递增区间为 -------------6分
-------------6分
(2)由(1)知
再由 得------------------------8分
得------------------------8分
 --------------------10分
--------------------10分
所以函数 的值域为
的值域为 -------------------------12分
-------------------------12分
18.(本小题满分12分)
(理) 解:(1)该考生得50分的情况有三类;①在“两道只能分别判断2个选项是错误的”时,该两题竟然全选对后面两道题全选错,其概率为 ;②在“两道只能分别判断2个选项是错误的”时,该两题竟然全选错后面两道题全选对,其概率为
;②在“两道只能分别判断2个选项是错误的”时,该两题竟然全选错后面两道题全选对,其概率为 ;③在“两道只能分别判断2个选项是错误的”时,该两题只能选对一道后面两道题也只能一错一对,其概率为
;③在“两道只能分别判断2个选项是错误的”时,该两题只能选对一道后面两道题也只能一错一对,其概率为 ,从而有
,从而有
 …………………………………4分
…………………………………4分
(2)用 表示所得分数,则
表示所得分数,则 可能的取值为40,45,50,55,60
可能的取值为40,45,50,55,60
∵



 ……………8分
……………8分
∴ 的概率分布列为
的概率分布列为

40
45
50
55
60
P





 …12分
…12分
(文) 解: (I)记“取到的4个球全是红球”为事件A,则

 ……………………… 4分
……………………… 4分
(II)记“取到的4个球至多有1个红球”为事件B,“取到的4个球只有1个红球”为事件

 由题意得
由题意得
 ………………………6分
………………………6分

 ………………………8分
………………………8分

 ………………………10分
………………………10分
所以,

化简,得
解得
n=2,或 故n=2. ………………………12分
故n=2. ………………………12分
19.(本小题满分12分)
证明: (I)连结PA.
∵ PD⊥平面ABCD, CD⊥AD,
∴ PA⊥CD(三垂线定理).………………2分
∵ M、N分别是PB、AB的中点,
∴ MN∥PA,
∴ MN⊥CD.………………………6分
(理)(II) 过点O作DN的垂线OE,垂足为E,连结ME.
∵ MO⊥平面ABCD,∴ ME⊥DN.
∴ ∠MEO就是二面角M-DN-C的平面角. ………………………9分
∵ △MOE中,∠MOE=90°,MO=3,OE= ,
,
∴  .
.
故二面角M-DN-C的大小为 .………………………12分
.………………………12分
(文)(II)设AC、BD交于点O.
∵ MO∥PD,
∴ MO⊥底面ABCD,且MO= PD=3.
PD=3.
………………………9分
∵ N是AB的中点,
∴  , ∴
, ∴ ,
,
∴  ………………………12分
………………………12分
20.(本小题满分12分)
(理) 解:(1)令 ,
,
则 ,---------------------------------------2分
,---------------------------------------2分
由 得,
得,
由 得,
得, ---------------------------------4分
---------------------------------4分
由 的定义域
的定义域 知,
知,
 的单调递增区间为
的单调递增区间为 ;递减区间为
;递减区间为 --------------------6分
--------------------6分
(2) 令 ,则函数
,则函数 与
与 的图象有且只有两个不同的交点
的图象有且只有两个不同的交点 与x轴正半轴有且只有两个不同的交点.对
与x轴正半轴有且只有两个不同的交点.对 求导数,得----------8分
求导数,得----------8分

 .
.
又∵x→0时, <0,x→+∞时,
<0,x→+∞时, >0------------------------------------------10分
>0------------------------------------------10分
 有两个不同正根的充要条件是
有两个不同正根的充要条件是 或
或
 ,解得m=7或m=
,解得m=7或m= .---------------------------12分
.---------------------------12分
也可由(1)知,函数 在
在 处取得极值,若要恰有两不同的根,则必有
处取得极值,若要恰有两不同的根,则必有 或
或 ,所以有m=7或m=
,所以有m=7或m=
(文)解:(Ⅰ)
 ,
,
 ---------------2分
---------------2分
 -----------------------------------4分
-----------------------------------4分
又
故所求 。----------------------6分
。----------------------6分
(Ⅱ)由(Ⅰ)知

由 得,
得, ,
,
由 得,
得,  ,
,
故函数 的单调递增区间为
的单调递增区间为 单调递减区间为
单调递减区间为 ------8分
------8分

 恒成立,
恒成立,
故函数 在单调递增区间为
在单调递增区间为 ---------------10分
---------------10分

由 得,
得, ,
,
由 得,
得,  ,
,
故函数 的单调递增区间为
的单调递增区间为 单调递减区间为
单调递减区间为 ----12分
----12分
21.(本小题满分12分)
(理)解:(1)由已知设椭圆方程为 ,
,
则 ---------------2分
---------------2分
 a=2, c=
a=2, c= ,
,  b=1.---------------------------------4分
b=1.---------------------------------4分
∴椭圆的标准方程为 ----------------------------------------------6分
----------------------------------------------6分
(2)当直线BC垂直于x轴时,BC=2,因此△ABC的面积S△ABC=1.
当直线BC不垂直于x轴时,说该直线方程为y=kx,代入 ,
,
解得B( ,
, ),C(-
),C(- ,-
,- ),------------8分
),------------8分
则 ,又点A到直线BC的距离d=
,又点A到直线BC的距离d= ,
,
∴△ABC的面积S△ABC=
于是S△ABC= ----------------------------10分
----------------------------10分
由 ≥-1,得S△ABC≤
≥-1,得S△ABC≤ ,其中,当k=-
,其中,当k=- 时,等号成立.
时,等号成立.
∴S△ABC的最大值是 .
-------------------------------12分
.
-------------------------------12分
(文)解:(Ⅰ)设 ,由
,由 知,点C的轨迹为
知,点C的轨迹为 .
.
由 消y,得
消y,得  .
.
设 ,
, ,则
,则 ,
, .………………………4分
.………………………4分
所以, ,
,
所以  ,
,
于是  .………………………………………………………6分
.………………………………………………………6分
(Ⅱ)假设存在过点P的弦EF符合题意,则此弦的斜率不为零,设此弦所在直线的方程为 .
.
由 消x,得
消x,得 .
.
设 ,
, ,则
,则 ,
, .…………………8分
.…………………8分
因为过点P作抛物线的弦的长度是原点到弦的中点距离的2倍,所以  ,
,
即 , ……………………10分
, ……………………10分
所以  ,得
,得  .
.
所以,存在 .………………………………………………………12分
.………………………………………………………12分
22.(本小题满分14分)
(理 )解:(I) 由已知,得  ,
,
即 , ………………………2分
, ………………………2分
所以数列{ }是公比为2的等比数列,首项为
}是公比为2的等比数列,首项为 =2,
=2,
故 =
= . ………………………4分
. ………………………4分
也可以用累积法
(II) 因为 =
= ,
,
若 =
= 恒成立,则
恒成立,则 恒成立,所以
恒成立,所以
 ………………………6分
………………………6分
解出 A=1,B=-4,C=6.
故存在常数A,B,C满足条件. ………………………8分
(III) =(b2-b1)+(b3-b2)+(b4-b3)+…+(bn+1-bn)=bn+1-b1
=(b2-b1)+(b3-b2)+(b4-b3)+…+(bn+1-bn)=bn+1-b1
=
=  ………………………11分
………………………11分
< 
=
= 
= 
≤  .………………………14分
.………………………14分
别证:可以应用数学归纳法.
(文) 解:(Ⅰ) ,
, . ---------------4分
. ---------------4分
(Ⅱ)∵ ,且
,且 ∴
∴ .-------------------------------8分
.-------------------------------8分
(Ⅲ)设第 个图形的边数为
个图形的边数为
∴ ,且
,且 , ∴
, ∴ .
.
∵第 个图形的面积为
个图形的面积为 则
则 ------------------------10分
------------------------10分
= =
=
∴

……

 ------------------------------------------12分
------------------------------------------12分
上述 个式子两边分别相加得:
个式子两边分别相加得:
 ]
]
∴
∴ -------------------------------------------------------------------14分
-------------------------------------------------------------------14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com