2006年广州市天河区中考综合练习
第一部分(选择题,共30分)
一、选择题(本大题共10小题,每小题3分,满分30分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
试题详情
(A) 3 (B) ±3 (C) -3 (D) ±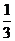
试题详情
试题详情
试题详情
3.一个不透明的袋中装有除颜色外均相同的5个红球和3个黄球,从中随机摸出一个,摸到黄球的概率是( ).
试题详情
试题详情
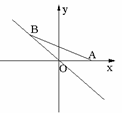
4.如图1,AB∥CD,AD,BC相交于O,∠BAD=35°,∠BOD=76°,则∠C的度数是( ).
试题详情
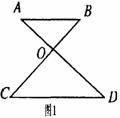 (A) 31° (B) 35° (C) 41° (D) 76°
(A) 31° (B) 35° (C) 41° (D) 76°
试题详情
5.方程 的根的情况是( ).
的根的情况是( ).
(A)有两个不等的实数根
(B) 有两个相等的实数根
(C) 没有实数根
(D) 有一个实数根
试题详情
6.已知两圆相切,其圆心距为6,大圆半径为8,则小圆半径r是( ).
(A) 2 (13) 14 (C) 6 (D) 2或14
试题详情
7.正比例函数图像经过点A(1,2),则该函数的解析式为( ).
试题详情
试题详情
8. 抛物线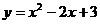 的顶点坐标是( ).
的顶点坐标是( ).
(A) (1,4) (B) (1,2) (c) (-1,4)
(D) (-1,-2)
试题详情
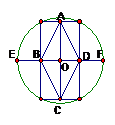
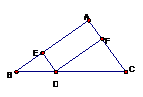
9.如图2,顺次连结圆内接矩形各边的中点,得到菱形ABCD,若BD=10,DF=4,则菱形ABCD的边长为( ).
试题详情
(A)4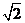 (B)5
(B)5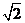 (C)6
(D)9.
(C)6
(D)9.
试题详情
10. 如图3,已知点A的坐标为(1,0),点B在直线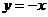 上运动,当线段AB最短时,点B的坐标为(
).
上运动,当线段AB最短时,点B的坐标为(
).
试题详情
试题详情
|
试题详情
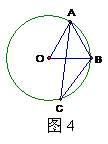
二、填空题(本大题共6小题,每小题3分,满分18分) 11.如图4,A、B、C是⊙O上的点,AB = 2┩,∠ACB=30°,那么⊙O的半径为____________┩. 试题详情
12.若一个二元一次方程组的解为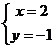 ,则这个方程组可以是________________(只要求写出一个) ,则这个方程组可以是________________(只要求写出一个) 试题详情
13.小刚每天骑自行车上学都要经过三个安装有红灯和绿灯的路口。假如每个路口红灯和绿灯亮的时间相同,那么,小刚从家随时出发去学校,他不遇红灯的概率是
. 试题详情
 14.已知圆锥的底面周长为20πcm,母线长为10cm,那么这个圆锥的侧面积是_________┩2(结果保留π). 14.已知圆锥的底面周长为20πcm,母线长为10cm,那么这个圆锥的侧面积是_________┩2(结果保留π).
试题详情
 15.已知二次函数y = ax2 +b( 15.已知二次函数y = ax2 +b(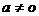 ,a,b是常数),x与y的部分对应值如下表, ,a,b是常数),x与y的部分对应值如下表,
那么方程ax2 +b
= 0的一个正的近似解是___________. x 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
0.21
|
|
|
|
|
|
|
试题详情
16.如图5,Rt△ABC中,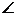 A=90 A=90 ,AB=4,AC=3,D在BC上运动(不与B、C重合),过D点分别作DE⊥AB于E、DF⊥AC于F,则矩形AEDF的面积的最大值为________. ,AB=4,AC=3,D在BC上运动(不与B、C重合),过D点分别作DE⊥AB于E、DF⊥AC于F,则矩形AEDF的面积的最大值为________. 试题详情
三、解答题(本大题共9小题,满分102分.解答应写出文字说明、证明过程或演算步骤.) 17.(本小题满分9分)求满足不等式 的一个正整数解 . 的一个正整数解 . 试题详情
18.(本小题满分9分)如图6,在⊙O中,弦AB与DC相交于点E,DB=AC. (1)求证:△AEC≌△DEB; (2)点B与点C是否关于直线OE对称?试说明理由. 试题详情
19.(本小题满分10分)解方程: 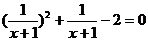 试题详情
20.(本小题满分10分) 图7是连续十周测试甲、乙两名运动员体能训练情况的折线统计图。教练组规定:体能测试成绩70分以上(包括70分)为合格。
图7 ⑵请从下面两个不同的角度对运动员体能测试结果进行判断: ①依据平均数与成绩合格的次数比较甲和乙, 的体能测试成绩较好; ②依据平均数与中位数比较甲和乙, 的体能测试成绩较好。 ⑶依据折线统计图和成绩合格的次数,分析哪位运动员体能训练的效果较好。
试题详情
平均数 中位数 体能测试成 绩合格次数 甲 65 乙 60
|
试题详情
试题详情
21.(本小题满分12分) 同学们对公园的滑梯很熟悉吧!如图8是某公园(六•一)前新增设的一台滑梯,该滑梯高度AC=2m,滑梯着地点B与梯架之间的距离BC=4m。 试题详情
(1)求滑梯AB的长(精确到0.1m); (2)若规定滑梯的倾斜角(∠ABC不超过45°属于安全范围).请通过计算说明这架滑梯的倾斜角是否属于安全范围? 试题详情
试题详情
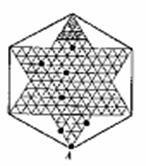
 , , 如图9(1)~(3)是跳棋盘,其中格点上的黑色点为棋子,剩余的格点上没有棋子.我们约定跳棋游戏的 如图9(1)~(3)是跳棋盘,其中格点上的黑色点为棋子,剩余的格点上没有棋子.我们约定跳棋游戏的 规则是:把跳棋棋子在棋盘内沿网格线隔着棋子对称跳行,跳行一次称为一步. 试题详情
(1) , , 如图9(1)已知点A为己方一枚棋子,欲将棋子A跳进对方区域(阴影部分的格点),则跳行的最少步数为( ) 如图9(1)已知点A为己方一枚棋子,欲将棋子A跳进对方区域(阴影部分的格点),则跳行的最少步数为( ) A.2步 B.3步 C.4步 D.5步 (2)如图9(2) 已知点C为己方一枚棋子,只给你一颗棋子在棋盘内任意摆放,能否把棋子C跳进对方区域(阴影部分的格点),请在图中描出摆放点并用字母O标明. 试题详情
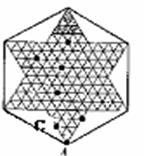 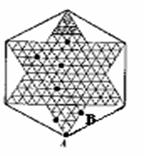 (3) 如图9(3)
已知点B为己方一枚棋子,给你两颗棋子在棋盘内任意摆放,将棋子B跳进对方区域(阴影部分的格点),请在图9(3)中描出摆放点且用字母M,N标明,然后画出跳行路线图. (3) 如图9(3)
已知点B为己方一枚棋子,给你两颗棋子在棋盘内任意摆放,将棋子B跳进对方区域(阴影部分的格点),请在图9(3)中描出摆放点且用字母M,N标明,然后画出跳行路线图.
试题详情
|
|
|
|
|
|
|
图9(1) 图9(2) 图9(3)
|
试题详情
已知:抛物线的解析式为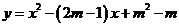 (1) 求证:此抛物线与x轴必有两个不同的交点; 试题详情
(2) 若此抛物线与直线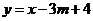 的一个交点在y轴上,求m的值。 的一个交点在y轴上,求m的值。 试题详情
24.(本小题满分14分) 有一根直尺的短边长2┩,长边长10┩,还有一块锐角为45°的直角三角形纸板,它的斜边长12cm..如图12,将直尺的短边DE放置与直角三角形纸板的斜边AB重合,且点D与点A重合.将直尺沿AB方向平移(如图13),设平移的长度为xcm(0≤x≤10),直尺和三角形纸板的重叠部分(图中阴影部分)的面积为S┩2. (1)当x=0时(如图12),S=_____________;当x = 10时,S =______________. (2) 当0<x≤4时(如图13),求S关于x的函数关系式; 试题详情
(3)当4<x<10时,求S关于x的函数关系式,并求出S的最大值(同学可在图14、图15中画草图). 试题详情
试题详情
试题详情
如图16-1,已知抛物线的顶点为A(O,1),矩形CDEF的顶点C、F在抛物线上,D、E在 轴上,CF交y轴于点B(0,2),且其面积为8. 轴上,CF交y轴于点B(0,2),且其面积为8. (1)求此抛物线的解析式; 试题详情
(2)如图16-2,若P点为抛物线上不同于A的一点,连结PB并延长交抛物线于点Q,过点P、Q分别作 轴的垂线,垂足分别为S、R. 轴的垂线,垂足分别为S、R. ①求证:PB=PS; ②判断△SBR的形状; ③试探索在线段SR上是否存在点M,使得△PSM≌△MRQ,若存在,请找出M点的位置;若不存在,请说明理由. 试题详情
试题详情
| | | | | | | | | | | |

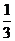
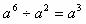 (B)
(B)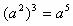 (C)
(C)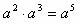 (D)
(D)
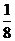 (B)
(B) 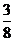 (C)
(C)
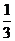 (D)
(D) 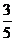
 (A) 31° (B) 35° (C) 41° (D) 76°
(A) 31° (B) 35° (C) 41° (D) 76° 的根的情况是( ).
的根的情况是( ).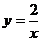 (13)
(13) 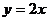 (C)
(C) 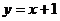 (D)
(D) 
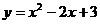 的顶点坐标是( ).
的顶点坐标是( ).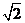 (B)5
(B)5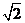 (C)6
(D)9.
(C)6
(D)9. 上运动,当线段AB最短时,点B的坐标为(
).
上运动,当线段AB最短时,点B的坐标为(
). (A)(0,0) (B)
(A)(0,0) (B)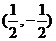 (c)
(c) 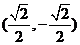 (D)
(D)  .
.
