
2006-2007学年度江苏省南京市二十九中初三第一学期调研试卷
一、选择题(每小题2分,共24分)
1.已知等腰三角形的一个底角等于30°,则这个等腰三角形的顶角等于( )
A.150° B.120° C.75° D.30°
2.方程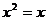 的解是( ).
的解是( ).
A.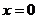 B.
B.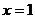 C.
C.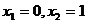 D.
D.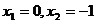
3.关于x的方程x2-2x+k=0有解,则k的值可以是( ).
A.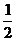 B.
B.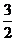 C.2
D.
C.2
D.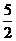
4.用配方法将方程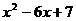 =0变形,结果正确的是 ( ).
=0变形,结果正确的是 ( ).
A.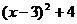 =0 B.
=0 B.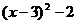 =0
=0
C.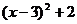 =0 D.)
=0 D.)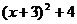 =0
=0
5.已知菱形的两条对角线长分别为
A.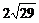 cm D.
cm D.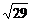 cm
cm
6.在一个四边形ABCD中,依次连结各边中点的四边形是菱形,则对角线AC与BD需要满足条件( )
A.垂直 B.相等 C.相交 D.不再需要条件
7.两直角边分别为3,4的直角三角形斜边上的高为( ).
A.3 B.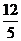
8.已知∠AOB=90°,点P在∠AOB的平分线上, OP=6,则点P到OA、OB的距离为( )
A.6、6 B.3、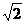 D. 3
D. 3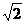 、3
、3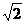
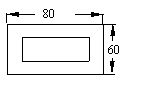
9.如图,从一块长方形铁片中间截去一个小长方形,使剩下部分四周的宽度都等于x,且小长方形的面积是原来长方形面积的一半,则x的值为( )
A.10 B.
10.平行四边形、矩形、菱形、正方形都具有的性质( )
A.对角线相等 B.对角线互相平分
C.对角线平分一组对角 D.对角线互相垂直
11.如图,在长为
A.
 |
12.商场服装柜在销售中发现:某童装平均每天可售出20件,每件盈利40元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施,调查发现:如果每件童装降价4元,那么平均每天就可多售出8件.要想平均每天销售这种童装共盈利1200元,设每件童装降价x元,那么应满足的方程是( ).
A.(40+x) (20-2x) =1200 B.(40-2x) (20+x) =1200
C.(40-x) (20+2x) =1200 D. (40+2x) (20-x) =1200
二、填空题(每小题3分,共12分)
13.等腰三角形的周长为7,一边长为1,则它另两边长分别为 .
14.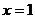 是关于x的方程
是关于x的方程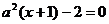 的解,则a=
.
的解,则a=
.
15.等腰三角形一腰上的高与另一腰的夹角为30°,若腰长为2,则腰上的高为 .
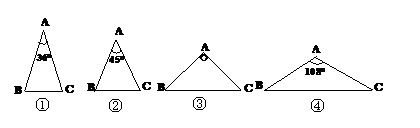
16.如图所示,在下列三角形中,若AB=AC,则能被一条直线分成两个小等腰三角形的
是 (填序号).
三、(每题6分,共24分)
17.解方程
(1)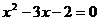 (2)
(2)
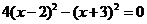
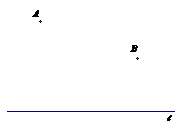 18.己知A、B两个电话分机离电话线l的距离如图所示,试用尺规在直线l确定一点P,使得点P到A、B两个电话分机的距离相等.
18.己知A、B两个电话分机离电话线l的距离如图所示,试用尺规在直线l确定一点P,使得点P到A、B两个电话分机的距离相等.
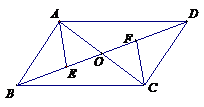 19.在平行四边形ABCD中,对角线AC、BD相交于点O,点E、F在BD上,且BE=DF,连结AE、FC,那么AE与FC有何关系?为什么?
19.在平行四边形ABCD中,对角线AC、BD相交于点O,点E、F在BD上,且BE=DF,连结AE、FC,那么AE与FC有何关系?为什么?
20.某农户种植花生,原来种植的花生亩产量为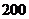 千克,出油率为
千克,出油率为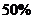 (即每
(即每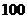 千克花生可加工成花生油
千克花生可加工成花生油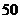 千克).现在种植新品种花生后,每亩收获的花生可加工成花生油
千克).现在种植新品种花生后,每亩收获的花生可加工成花生油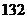 千克,其中花生出油率的增长率是亩产量增长率的
千克,其中花生出油率的增长率是亩产量增长率的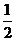 ,求新品种花生亩产量的增长率.
,求新品种花生亩产量的增长率.
四、(每小题6分,共12分)
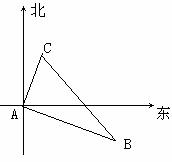
21.甲、乙两船同时从港口A出发,甲船以12海里/时的速度向北偏东35°航行,乙船向南偏东55°航行。2小时后,甲船到达C岛,乙船到达B岛,若C、B两船相距40海里,问乙船的速度是每小时多少海里?
22. 如图,有一地面为长方形的仓库,一边长为

五、(第23题7分,第24题8分,共15分)
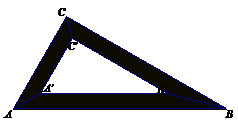
23.如图,一块含有30º角(∠ABC=30º,∠ACB=90º)的木制三角板是由三块宽度相等的木条拼合而成,若木条的宽度为
 |
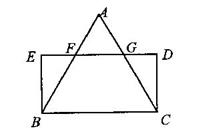 24.已知:如图,△ABC中,AB=AC,矩形BCDE的边DE分别与AB、AC交于点F,G。求证:EF=DG.
24.已知:如图,△ABC中,AB=AC,矩形BCDE的边DE分别与AB、AC交于点F,G。求证:EF=DG.
六、(每小题8分,共16分)
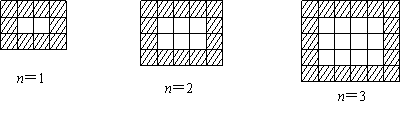
25.如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,观察下列图形并解答有关问题:
(1)在第n个图中,共有 块白色瓷砖,共有 块黑色瓷砖(均用含n的代数式表示);
(2)若铺设这样的矩形地面共用了506块瓷砖,通过计算求此时n的值;
(3)是否存在n,使得黑瓷砖与白瓷砖块数相等的情形?说明理由。
 |
26. 在劳技课上,老师请同学们在一张长为
 |
 |
||
七、(本题8分)
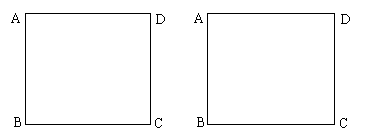
 27.如图,折叠矩形纸面ABCD,先折出折痕(对角线)BD,再折叠,使AD落在对角线BD上,得折痕DE,若3AB=4BC,AE=1,求AB的长.
27.如图,折叠矩形纸面ABCD,先折出折痕(对角线)BD,再折叠,使AD落在对角线BD上,得折痕DE,若3AB=4BC,AE=1,求AB的长.
八、(本题9分)
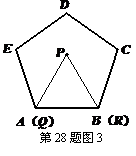
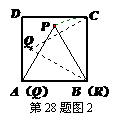 例如:如图2,边长为1的等边三角形PQR的顶点P在边长为1的正方形ABCD内,顶点Q与点A重合,顶点R与点B重合,△PQR沿着正方形ABCD的边BC、CD、DA、AB……连续转动,当△PQR连续转动3次时,顶点P回到正方形ABCD内部,第一次出现P的“点回归”;当△PQR连续转动4次时△PQR回到原来的位置,出现第一次△PQR 的“三角形回归”.
例如:如图2,边长为1的等边三角形PQR的顶点P在边长为1的正方形ABCD内,顶点Q与点A重合,顶点R与点B重合,△PQR沿着正方形ABCD的边BC、CD、DA、AB……连续转动,当△PQR连续转动3次时,顶点P回到正方形ABCD内部,第一次出现P的“点回归”;当△PQR连续转动4次时△PQR回到原来的位置,出现第一次△PQR 的“三角形回归”.
操作:如图3,如果我们把边长为1的等边三角形PQR沿着边长为1的正五边形ABCDE的边连续转动,则连续转动的次数
k= 时,第一次出现P的“点回归”;连续转动的次数k= 时,第一次出现△PQR 的“三角形回归”.
猜想:
我们把边长为1的等边三角形PQR沿着边长为1的正n(n>3)边形的边连续转动,
(1)连续转动的次数k= 时,第一次出现P的“点回归”;
(2)连续转动的次数k= 时,第一次出现△PQR 的“三角形回归”;
(3)第一次同时出现P的“点回归”与△PQR 的“三角形回归”时,写出连续转动的次数k与正多边形的边数n之间的关系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com