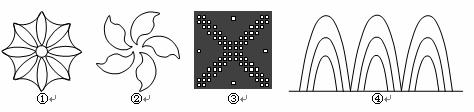
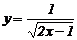(第05题图) A、①② B、①③ C、②③ D、①②③
试题详情
6.顺次连接等腰梯形四边中点所得到的四边形是( ). A、等腰梯形
B、直角梯形
C、矩形
D、菱形 试题详情
7.“圆柱与球的组合体”如图所示,则它的三视图是( ). 试题详情
试题详情
试题详情
8.二次函数y=ax2+bx+c图象如图所示,则点A(ac,bc)在( ). 试题详情
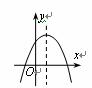
A、第一象限
B、第二象限
C、第三象限
D、第四象限 试题详情
9.如图,正方形ABCD内接于⊙O,点E在劣弧AD上,则∠BEC等于( ). 试题详情
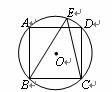
A、45°
B、60°
C、30°
D、55° 试题详情
10.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下( ). A、小明的影子比小强的影子长
B、小明的影子比小强的影子短 C、小明的影子和小强的影子一样长 D、无法判断谁的影子长 试题详情
11.已知k1<0<k2,则函数y=k1x和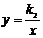 的图象大致是( ). 的图象大致是( ). 试题详情
试题详情
12.如图,小丽自己动手做了一顶圆锥形的圣诞帽,母线长是30cm,底面半径是10cm,她想在帽子上缠一根漂亮的丝带,从A出发绕帽子侧面一周,至少需要丝带( ). 试题详情
试题详情
试题详情
二.填空题(本题共8个小题,每小题4分,共32分,请把答案填在题中的横线上.) 13.如图是一个小熊的图像,图中反映出圆与圆的四种位置关系,但是其中有一种位置关系没有反映出来,请你写出这种位置关系,它是____________. 试题详情
试题详情
14.老师给出了一个函数,甲、乙、丙三位同学分别指出了这个函数的一个性质,甲:第一象限内有它的图象;乙:第三象限内有它的图象;丙:在每个象限内,y随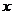 的增大而减小。请你写一个满足上述性质的函数解析式_________________. 的增大而减小。请你写一个满足上述性质的函数解析式_________________. 试题详情
15.兰州市政府为解决老百姓看病难的问题,决定下调药品的价格,某种药品经过两次降价,由每盒72元调至56元.若每次平均降价的百分率为x,由题意可列方程为_________________. 试题详情
16.将抛物线y=2x2先沿x轴方向向左平移2个单位,再沿y轴方向向下平移3个单位,所得抛物线的解析式是___________________. 试题详情
17.赵亮同学想利用影长测量学校旗杆的高度,如图,他在某一时刻立1米长的标杆测得其影长为1.2米,同时旗杆的投影一部分在地面上,另一部分在某一建筑的墙上,分别测得其长度为9.6米和2米,则学校旗杆的高度为___________米. 试题详情
试题详情
18.抛物线y=ax2+2ax+a2+2的一部分如图所示,那么该抛物线在y轴右侧与x轴交点的坐标是_____________. 试题详情
试题详情
19.如图,PA、PB切⊙O于A、B两点,若∠APB=60°,⊙O的半径为3,则阴影部分的面积为_____. 试题详情
试题详情
20.下列是三种化合物的结构式及分子式,请按其规律,写出后一种化合物的分子式为___________. 试题详情
试题详情
三.作图题(本题满分5分,要求尺规作图,不写作法和证明,但保留作图痕迹.) 21.在Rt△ABC中,∠ACB=90°,∠CAB=30°,用两种方法把它分成两个三角形,且要求一个三角形是等腰三角形. 试题详情
试题详情
四.解答题(本大题共9道题,共计65分,解答时写出必要的文字说明、证明过程或演算步骤.)
试题详情
计算:0.25×(-cos60°)-2-(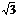 -1)0+tan60° -1)0+tan60° 试题详情
试题详情
试题详情
试题详情
将背面相同,正面分别标有数字1、2、3、4的四张卡片洗匀后,背面朝上放在桌子上. (1)从中随机抽取一张卡片,求该卡片正面上的数字是偶数的概率; (2)先从中随机抽取一张卡片(不放回),将该卡片正面上的数字作为十位上的数字;再随机抽取一张,将该卡片正面上的数字作为个位上的数字,则组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明. 试题详情
25.(本题满分7分) 如图,已知AB是⊙O的直径,弦CD⊥AB,垂足为H. (1)求证:AH•AB=AC2; (2)若过A的直线与弦CD(不含端点)相交于点E,与⊙O相交于点F,求证:AE•AF=AC2; (3)若过A的直线与直线CD相交于点P,与⊙O相交于点Q,判断AP•AQ=AC2是否成立(不必证明). 试题详情
试题详情
26.(本题满分7分) 兰州市某校对九年级学生进行“综合素质”评价,评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级.现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理,并作出如图所示的统计图,已知图中从左到右的四个长方形的高的比为:14∶9∶6∶1,评价结果为D等级的有2人,请你回答以下问题: (1)共抽测了多少人? (2) 样本中B等级的频率是多少?C等级的频率是多少? (3)如果要绘制扇形统计图,A、D两个等级在扇形统计图中所占的圆心角分别是多少度? (4)该校九年级的毕业生共300人,假如“综合素质”等级为A或B的学生才能报考示范性高中,请你计算该校大约有多少名学生可以报考示范性高中? 试题详情
试题详情
27.(本题满分7分) 某农场计划建一个养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙(墙足够长),另外的部分用30米的竹篱笆围成,现有两种方案:①围成一个矩形(如下左图);②围成一个半圆形(如下右图).设矩形的面积为S1平方米,宽为x米,半圆形的面积为S2平方米,半径为r米,请你通过计算帮助农场主选择一个围成区域面积最大的方案(π≈3). 试题详情
试题详情
28.(本题满分8分) 兰州市城市规划期间,欲拆除黄河岸边的一根电线杆AB(如图),已知距电线杆AB水平距离14米处是河岸,即BD=14米,该河岸的坡面CD的坡角∠CDF的正切值为2,岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将此人行道封上?(在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域) 试题详情
试题详情
29.(本题满分9分) 如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF. (1)求证:四边形DAEF是平行四边形; (2)探究下列问题:(只填满足的条件,不需证明) ①当△ABC满足_________________________条件时,四边形DAEF是矩形; ②当△ABC满足_________________________条件时,四边形DAEF是菱形; ③当△ABC满足_________________________条件时,以D、A、E、F为顶点的四边形不存在. 试题详情
试题详情
30.(本题满分10分) 已知抛物线y=ax2+bx+c的图象交x轴于点A(x0,0)和点B(2,0),与y轴的正半轴交于点C,其对称轴是直线x=-1,tan∠BAC=2,点A关于y轴的对称点为点D. (1)确定A、C、D三点的坐标; (2)求过B、C、D三点的抛物线的解析式; (3)若过点(0,3)且平行于x轴的直线与(2)小题中所求抛物线交于M、N两点,以MN为一边,抛物线上任意一点P(x,y)为顶点作平行四边形,若平行四边形的面积为S,写出S关于P点纵坐标y的函数解析式. 试题详情
(4)当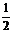 <x<4时,(3)小题中平行四边形的面积是否有最大值,若有,请求出,若无,请说明理由. <x<4时,(3)小题中平行四边形的面积是否有最大值,若有,请求出,若无,请说明理由. 试题详情
| 
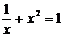
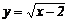 B、
B、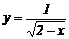 C、
C、 D、
D、