
2007-2008学年度烟台市栖霞第一学期质量检测
九年级数学质量检测试题
(时间:90分钟;满分150分)
一、选择题 (每小题4分,共48分,每小题有且只有一个正确答案)
1.给出下列函数:(1)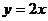 (2)
(2)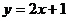 (3)
(3)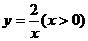 (4)
(4)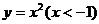 .其中,y随
.其中,y随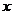 的增大而减小的函数是
( )
的增大而减小的函数是
( )
(A)(1)、(2) (B)(1)、(3)
(C)(3)、(4) (D)(2)、(3)、(4)
2.打开某洗衣机开关,在开始洗涤衣服时(洗衣机内无水),洗衣机经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间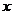 (分钟)之间满足某种函数关系,其函数图象大致为( )
(分钟)之间满足某种函数关系,其函数图象大致为( )
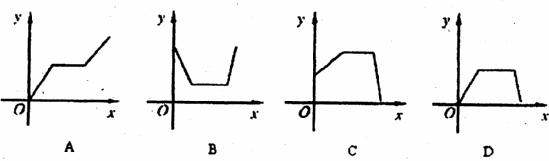
3.下列四幅图形中,表示两颗圣诞树在同一时刻阳光下的影子的图形可能是( )

4.两圆有多种位置关系,下图中不存在的位置关系是( )
A.外离 B.外切 C.相交 D.内切
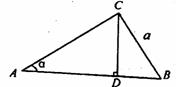
5.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,已知BC=a,∠A=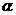 ,则CD的长可表示为 ( )
,则CD的长可表示为 ( )
A.a?sin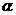 B.a?cos
B.a?cos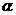 C.a?tan
C.a?tan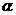 D.
D.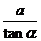
6.已知圆锥的侧面积为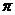 cm2,底面半径为3cm,则圆锥的高是( )
cm2,底面半径为3cm,则圆锥的高是( )
A.3cm B.4cm C.5cm D.8cm
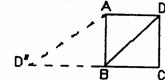
7.如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D’处。那么tan∠BD’A等于( )
A.1 B.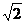 C.
C.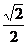 D.
D.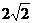
8.若函数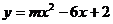 的图象与
的图象与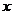 轴只有一个公共点,则m的取值范围是( }
轴只有一个公共点,则m的取值范围是( }
A.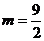 B.
B.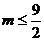 C.
C.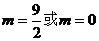 D.
D.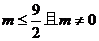
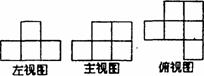
9.一仓库管理员需要清点仓库的物品,物品全是一些大小相同的正方体箱子,他不能搬下箱子进行清点。后来,他想出了一个办法,通过观察物品的三视图求出了仓库里的存货.他所看到的三视图如下图.仓库管理员清点出存货的个数是( )
A.5 B.6 C.7 D.8
10.在“五?一”黄金周期间,某超市推出如下购物优惠方案:(1)一次性购物在100元(不含100元)以内时,不享受优惠;(2)一次性购物在100元(含100元)以上,300元(不含300元)以内时,一律享受九折的优惠;(3)一次性购物在300元(含300元)以上时,一律享受八折的优惠.
王茜在本超市两次购物分别付款80元、252元.如果王茜改成在本超市一次性购买与上两次完全相同的商品,则应付款( )
A.332元 B.316元或332元 C.288元 D.288元或316元
11.两圆的半径恰好是方程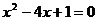 的两个根,当这两圆相交时,圆心距d的取值范围是( )
的两个根,当这两圆相交时,圆心距d的取值范围是( )
A.d<4 B.1<d<4 C.2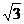 <d<4 D.d>2
<d<4 D.d>2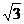
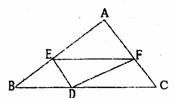
12.如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC边上一个动点,EF//BC,交AB于点E,交AC于点F,设E到BC的距离为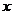 ,△DEF的面积为y,则y关于
,△DEF的面积为y,则y关于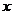 的函数图象大致为( )
的函数图象大致为( )
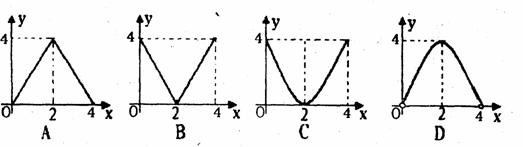
二:填空题(每小题4分,共24分)
13.如果一个立体图形的主视图为矩形,则这个立体图形可能是 .(只需填上一个立体图形).
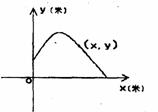
14.一个运动员推铅球时,铅球沿抛物线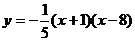 的路线行进,其图像如图所示.则铅球推出的距离为
米.
的路线行进,其图像如图所示.则铅球推出的距离为
米.
15.一组数据5,7,7,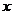 的中位数与平均数相等,则
的中位数与平均数相等,则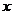 的值为
.
的值为
.
16.为改善市区人居环境,某市建设污水管网工程.已知圆柱形污水管的直径为50cm,截面如图所示.当管内污水的面宽AB=40cm时,污水的最大深度为 cm.
17.如图,∠1的余弦值等于 。
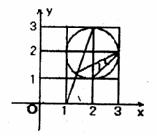
18.将一副直角三角尺如图摆放在一起,若BC=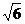 ,则AD=
,则AD=
三、解答题(本大题8个小题,满分78分.要写出必要的文字说明、证明过程或演算步骤)
19.(本小题满分6分)计算: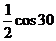 °
°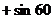 °
°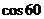 °
°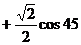 °
°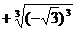
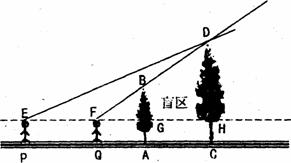
20.(本小题满分8分)如图,两颗树的高度分别为AB=6m,CD=8m,两树的根部间的距离AC=4m,小强沿着正对这两棵树的方向从左向右前进,如果小强的眼睛与地面的距离为l.6m.当小强与树AB的距离小于多少时,就不能看到树CD的树顶D?
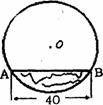
21.(本题满分9分)已知二次函数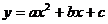 的图像如图所示,顶点为M,ON=2,MN=1,OB?OC=3。
的图像如图所示,顶点为M,ON=2,MN=1,OB?OC=3。
求:(1)a、b、c的值;
(2)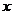 为何值时,y>0;
为何值时,y>0;
(3)求S△ABC.
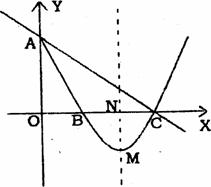
22.(本小题满分9分)如图,是一块从生日蛋糕中切下的锲型蛋糕.
(1)计算扇形OAD的面积;
(2)计算锲型的体积;
(3)计算锲型蛋糕的整个表面积.
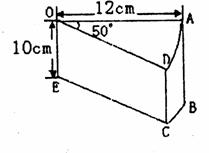
23.(本小题满分10分)如图,在小岛上有一观察站A.据测.灯塔B在观察站A北偏西45°的方向,灯塔C在B正东方向,且相距l 0海里,灯塔C与观察站A相距10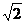 海里,请你测算灯塔C处在观察站A的什么方向?
海里,请你测算灯塔C处在观察站A的什么方向?

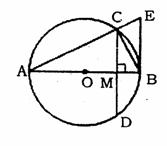
24.(本小题满分11分) 如图,AB为⊙O的直径,弦CD⊥AB于点M,过点B作BE//CD,交AC的延长线于点E,连结BC。
(1)求证:BE为⊙O的切线;
(2)如果CD=6,tan∠BCD=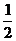 ,求⊙O的直径.
,求⊙O的直径.
25.(本小题满分12分)春、秋季节,由于冷空气的入侵,地面气温急剧下降到0℃以下的天气现象称为“霜冻”;由霜冻导致植物生长受到影响或破坏现象称为霜冻灾害,某种植物在气温是0℃以下持续时间超过3小时,即遭到霜冻灾害,需采取预防措施,下图是气象台某天发布的该地区气象信息,预报了次日0时―8时气温随着时间变化情况,其中0时―5时的图象满足一次函数关系,5时―8时的图象满足函数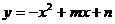 (5≤x≤8)关系.请你根据图中信息,解答下列问题:
(5≤x≤8)关系.请你根据图中信息,解答下列问题:
(1)求次日5时的气温;
(2)求函数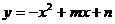 (5≤x≤8)的解析式;
(5≤x≤8)的解析式;
(3)针对这种植物判断次日是否需要采取防霜措施,并说明理由.
(参学数据: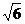 ≈2.449)
≈2.449)

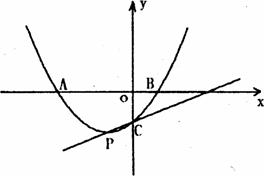
26.(本题满分l 3分)如图,抛物线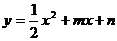 交
交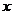 轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是一3,点B的横坐标是1.
轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是一3,点B的横坐标是1.
(1)求m、n的值;
(2)求直线PC的解析式;
(3)请探究以点A为圆心、直径为5的圆与直线PC的位置关系,并说明理由.
(参考数: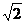 ≈l.41,
≈l.41,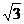 ≈1.73,
≈1.73,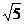 ≈2.24)
≈2.24)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com