
2008年滨州市中等学校招生考试
数学试题
一、选择题
1、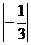 的相反数是( )
的相反数是( )
A、-3
B、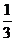 D、-
D、-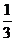
2、只用下列图形不能镶嵌的是( )
A、三角形 B、四边形 C、正五边形 D、正六边形
3、下列计算结果正确的是( )
A、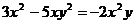 B、
B、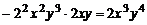
C、28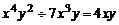 D、
D、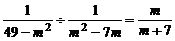
4、在平面直角坐标系中,若点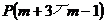 在第四象限,则m的取值范围为( )
在第四象限,则m的取值范围为( )
A、-3<m<1 B、m>
5、若关于x的一元二次方程(m-1)x2+5x+m2
A、1
B、
6、将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线剪去上方的小三角形。

将纸片展开,得到的图形是( )

A B C D
7、某书店把一本新书按标价的九折出售,仍可获利20%,若该书的进价为21元,则标价为( )
A、26元 B、27元 C、28元 D、29元
8、如图,一个空间几何体的主视图和左视图都是边长为1的三角形,俯视图是一个圆,那么这个几何体的侧面积是( )

A、 B、
B、 C、
C、 D、
D、
9、“上升数”是一个数中右边数字比左边数字大的自然数(如:34,568,2469等),任取一个别两位数,是“上升数”的概率是( )
A、 B、
B、 C、
C、 D、
D、
10、如图1,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图2所示,则△ABC的面积是( )

图1 图2
A、10 B、
11、若A(-4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-5的图象上的三点,则y1,y2,y3的大小关系是( )
A、y1<y2<y3 B、y2<y1<y
12、如图所示,AB是⊙O的直径,AD=DE,AE与BD交于点C,则图中与∠BCE相等的角有( )
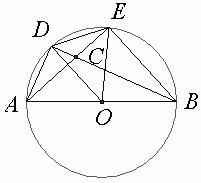
A、2个 B、3个 C、4个 D、5个
二、填空题
13、在2008年北京奥运会国家体育场的“鸟巢”钢结构工程施工建设中,首次使用了我国科研人员自主研制的强度为4.581亿帕的钢材.4.581亿帕用科学计数法表示为_____________帕(保留两位有效数字).
14、如图,已知AB∥CD,BE平分∠ABC,∠CDE=150°,则∠C=________________.
15、分解因式:(
16、将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,……如此继续下去,结果如下表:
所剪次数
1
2
3
4
…
n
正三角形个数
4
7
10
13
…
an
则an=________________(用含n的代数式表示).
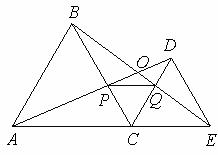
17、如上右图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.恒成立的结论有_______________________(把你认为正确的序号都填上)。
三、解答题
18、已知一次函数的图像过点(1,1)与(2,-1),求这个函数的解析式并求使函数值为正值的x的范围.
19.(本题满分8分)四川汶川大地震牵动了三百多万滨州人民的心,全市广大中学生纷纷伸出了援助之手,为抗震救灾踊跃捐款。滨州市振兴中学某班的学生对本校学生自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据。下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为3:4:5:8:6,又知此次调查中捐款25元和30元的学生一共42人。
(1)他们一共调查了多少人?
(2)这组数据的众数、中位数各是多少?
(3)若该校共有1560名学生,估计全校学生捐款多少元?

20.(本题满分8分)
为迎接2008年奥运会,某工艺厂准备生产奥运会标志“中国印”和奥运会吉祥物“福娃”。该厂主要用甲、乙两种原料,已知生产一套奥运会标志需要甲原料和乙原料分别为4盒和3盒;生产一套奥运会吉祥物需要甲原料和乙原料分别为5盒和10盒。该厂购进甲、乙原料的量分别为20000盒和30000盒,如果所进原料全部用完,求该厂能生产奥运会标志和奥运会吉祥物各多少套?
21.(本题满分10分)
在梯形ABCD中,AB∥CD, ,AB=2,BC=3,CD=1,E是AD中点,试判断EC与EB的位置关系,并写出推理过程。
,AB=2,BC=3,CD=1,E是AD中点,试判断EC与EB的位置关系,并写出推理过程。

22、如图,AC是某市坏城路的一段,AE、BF、CD都是南北方向的街道,其与环城路AC的交叉路口分别是A、B、C经测量花卉世界D位于点A的北偏东45°方向,点B的北偏东30°方向上,AB=
(1)求∠ADB的大小;
(2)求B、D之间的距离;
(3)求C、D之间的距离.

23、(1)探究新知:
如图1,已知△ABC与△ABD的面积相等,试判断AB与CD的位置关系,并说明理由.
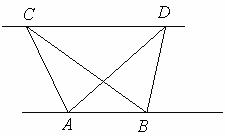
图1
(2)结论应用:
①如图2,点M、N在反比例函数y=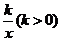 的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试应用(1)中得到的结论证明:MN∥EF.
的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F.试应用(1)中得到的结论证明:MN∥EF.
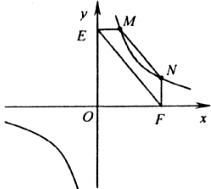
图2
②若①中的其他条件不变,只改变点M,N的位置如图3所示,请判断MN与E是否平行.
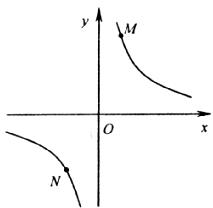
图3
24.(本题满分12分)
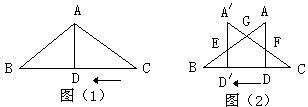
如图(1),已知在△ABC中,AB=AC=10,AD为底边BC上的高,且AD=6。将△ACD沿箭头所示的方向平移,得到△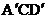 。如图(2),
。如图(2),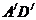 交AB于E,
交AB于E, 分别交AB、AD于G、F。以
分别交AB、AD于G、F。以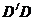 为直径作⊙O,设
为直径作⊙O,设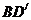 的长为x,⊙O的面积为y。
的长为x,⊙O的面积为y。
(1)求y与x之间的函数关系式及自变量x的取值范围;
(2)连结EF,求EF与⊙O相切时x的值;
(3)设四边形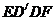 的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?
的面积为S,试求S关于x的函数表达式,并求x为何值时,S的值最大,最大值是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com